Introduction to Analysis of Algorithms

Here are a series of slides and codes in the subject of Analysis of Algorithms

Lab of Analysis of Algorithms

Here is the Lab for the class of algorithms Lab Page

Classic Analysis of Algorithms

1. Introduction Slides Notes
   • Why the need for algorithms?
   • Basic Algorithms for this class
   • Some Note in Notation
   • An example of analyzing algorithms

   

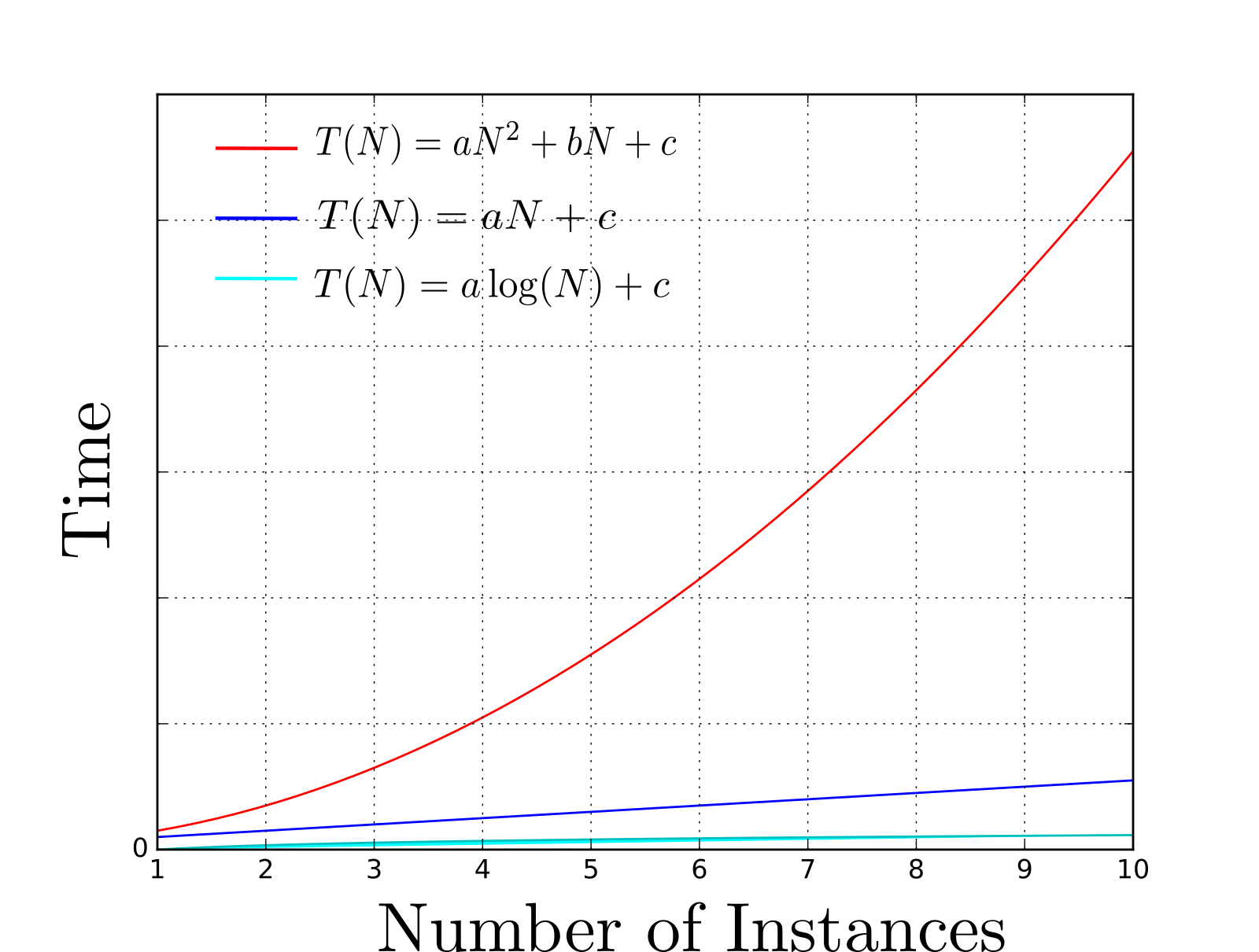
2. Math for Analysis of Algorithms Slides
   • A simple introduction to the necessary math
     • Discrete Mathematics
     • Probability
   \[P(X=x_{j})=P(s_{j}\in S\vert X(s_{j})=x_{j})\]
3. Divide and Conquer Slides Notes
   • The Recursion and the Induction
   • Using Induction to Prove Algorithm Correctness
   • Asymptotic Notation
   • Methods to solve recursion
     • Substitution
     • Recursion Tree Method
     • The Master Method

   

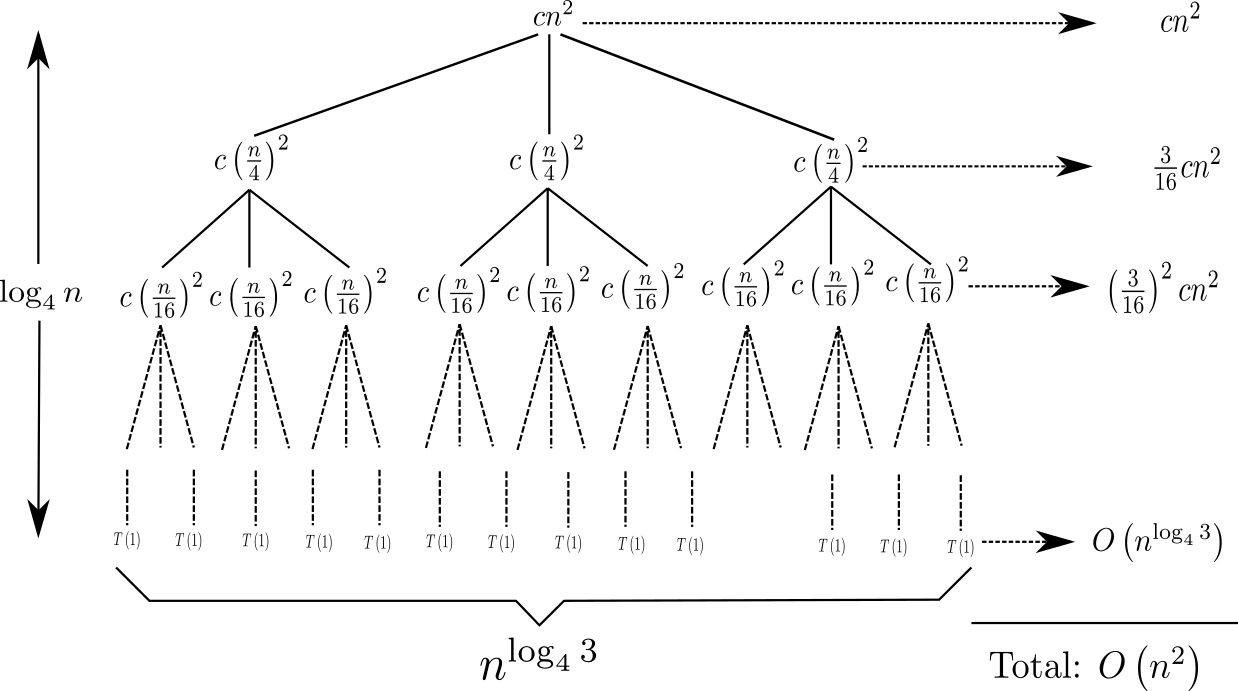
4. Probability Analysis Slides Notes
   • The Hiring Problem
   • Indicator Random Variables
   • Randomized Hiring
   • Enforcing Randomization
   \[E\left[X_{A}\right]=Pr\left\{ A\right\}\]
5. Sorting Slides Notes
   • Sorting Problem
   • Heaps
   • Quicksort
   • Randomized Quicksort
   • Lower Bounds of Sorting

   

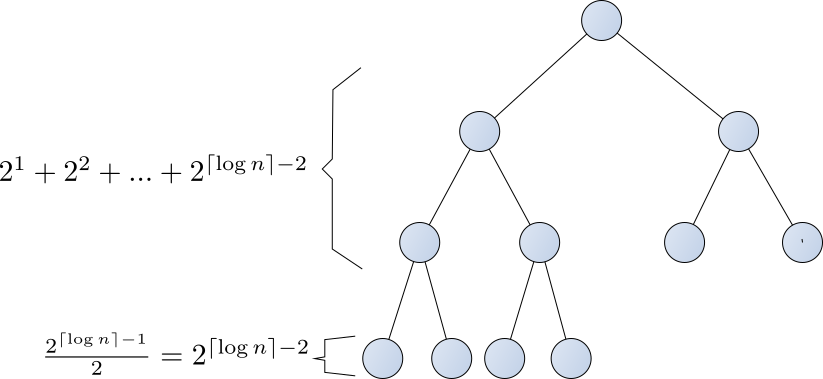
6. Linear Sorting Slides Notes
   • Counting Sort
   • Least Significant Digital Radix Sort
   • Bucket Sort

   

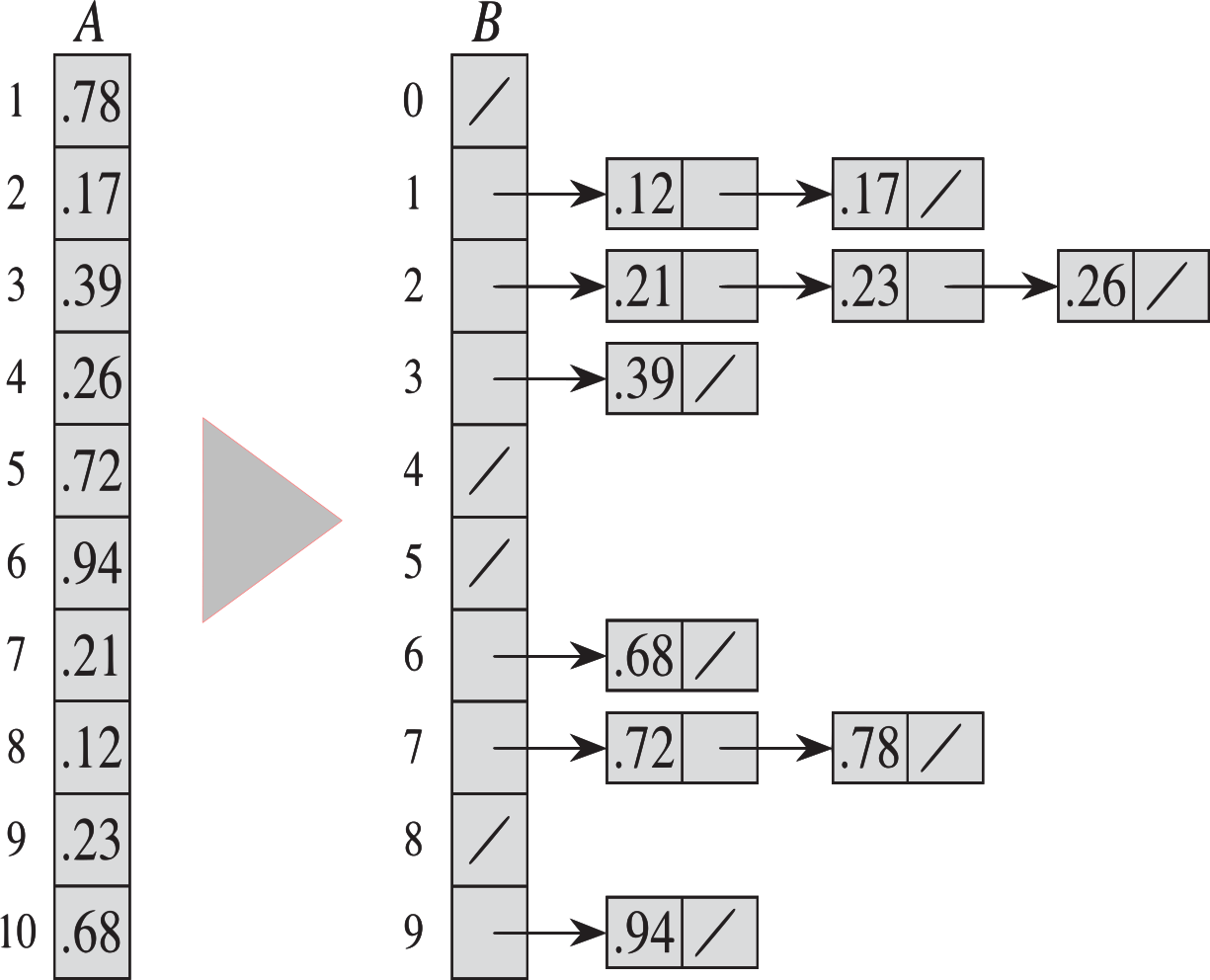
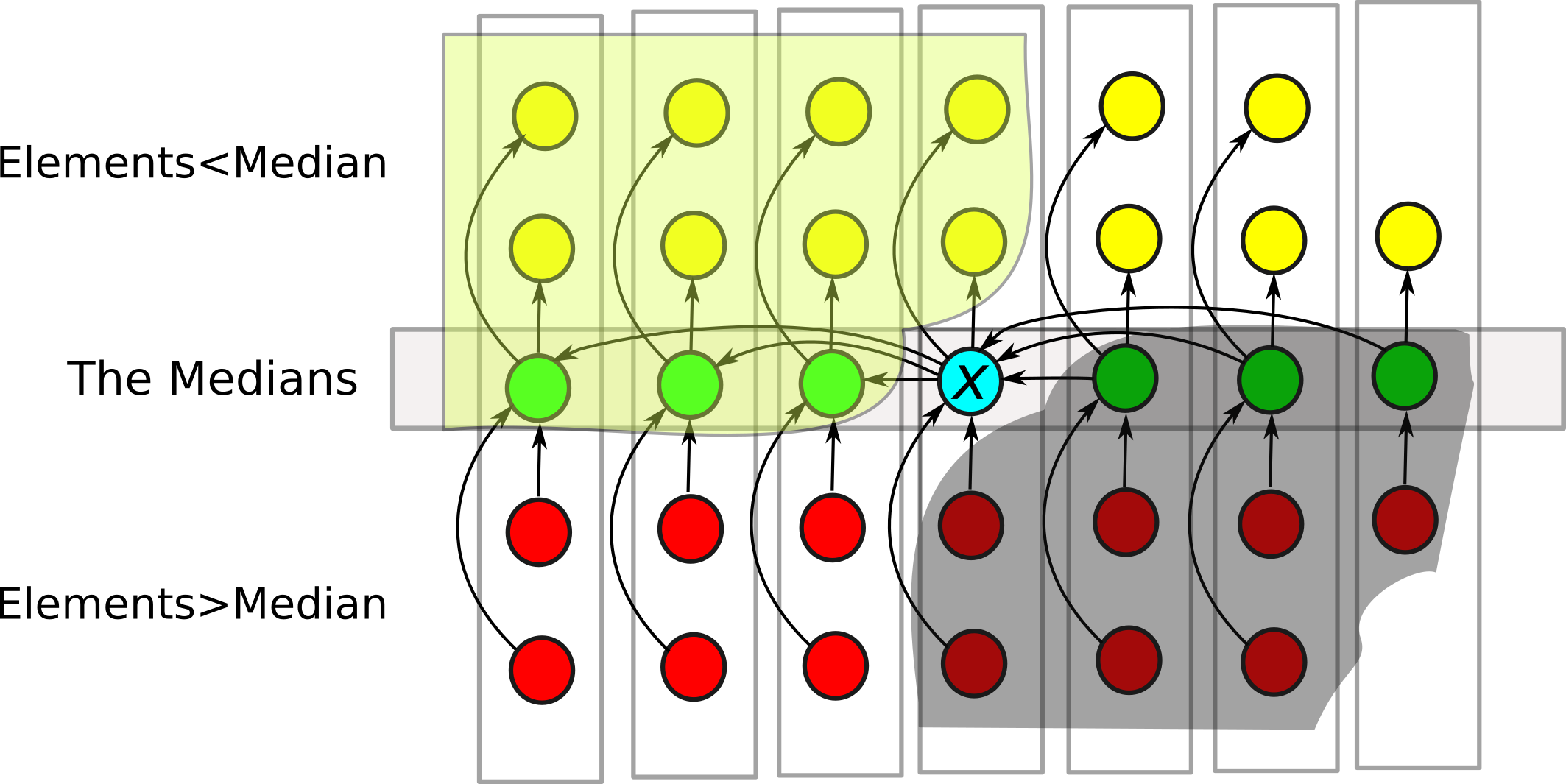
7. Median Order Statistics Slides Notes
   • kth statistics
   • Using Randomization
   • Worst Case
   • Final Worst Case

   

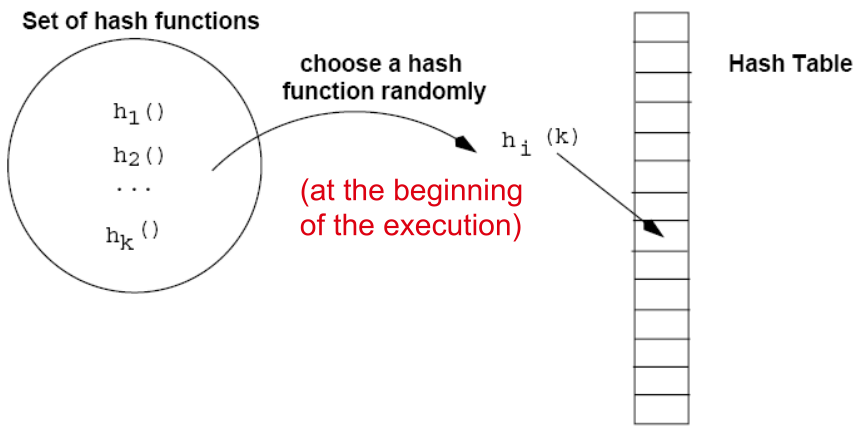
8. Hash Tables Slides Notes
   • Introduction to Hash Tables
   • The Hashing Methods
   • Clustering Analysis of Hashing Functions
   • A possible Solution, Universal Hashing
   • Open Addressing

   

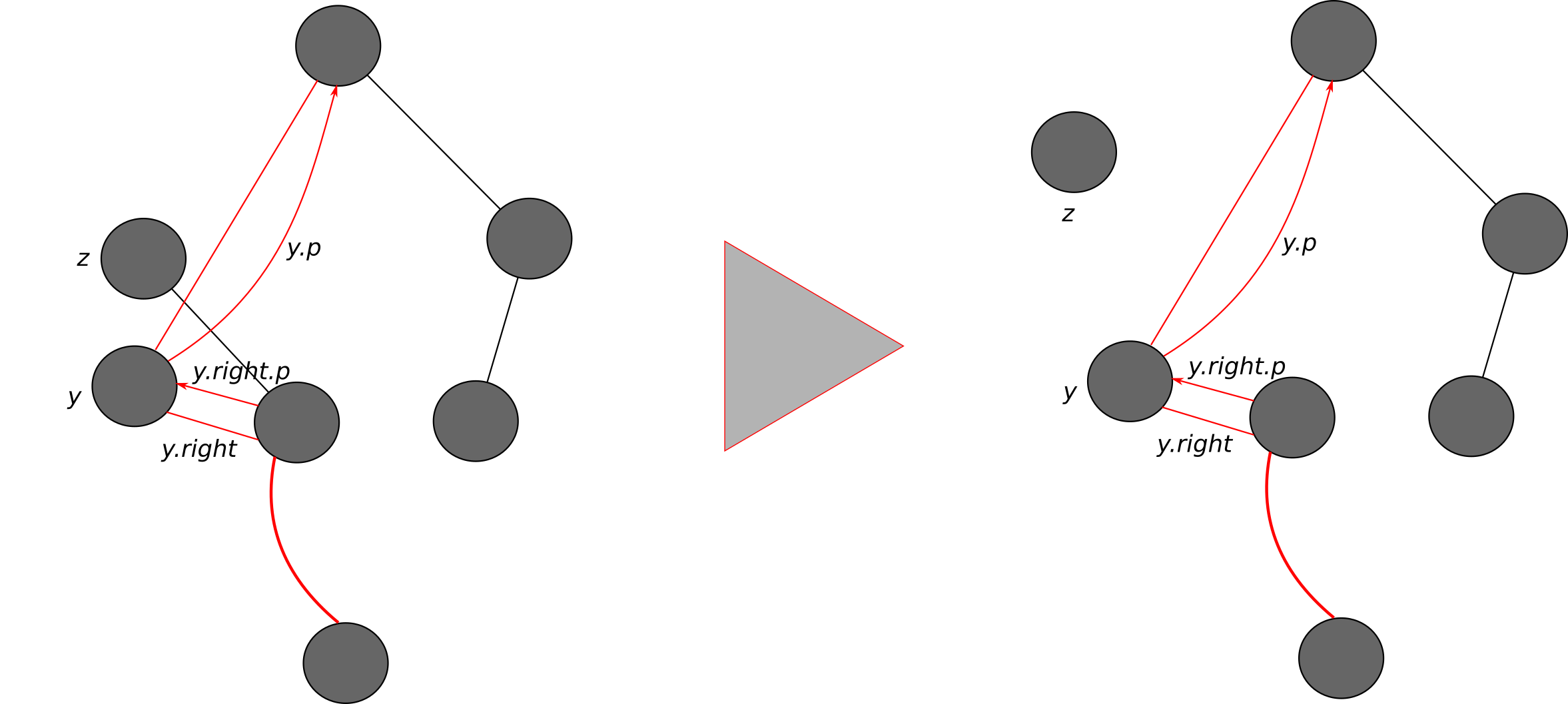
9. Binary Trees Slides Notes
   • Basic Concepts
   • Binary Search Trees
   • Balancing Trees AVL

   

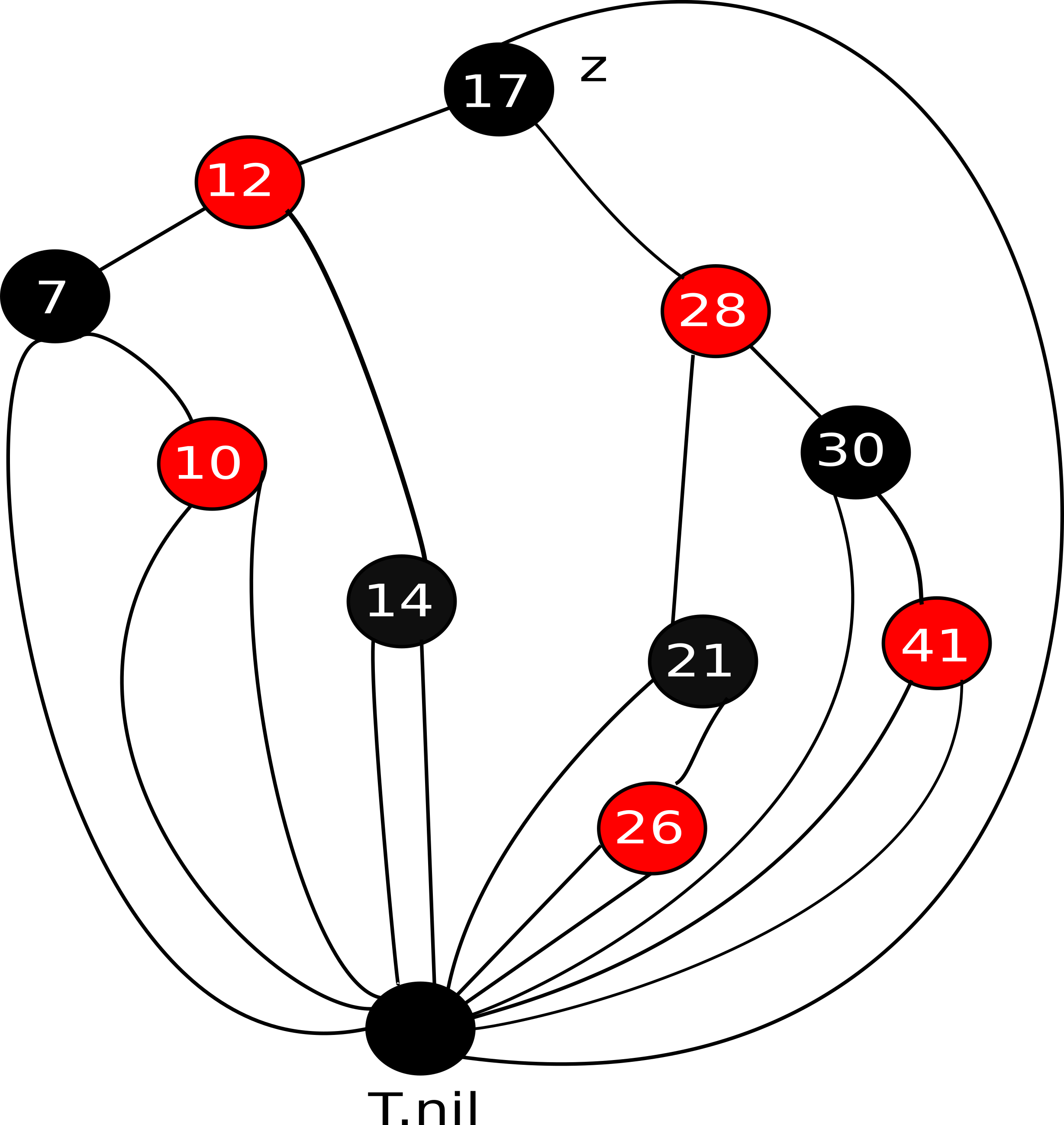
10. Red Black Trees Slides Notes
    • Basic Definitions
    • Insertion in Red Black Trees
    • Deletion in Red Black Trees

    

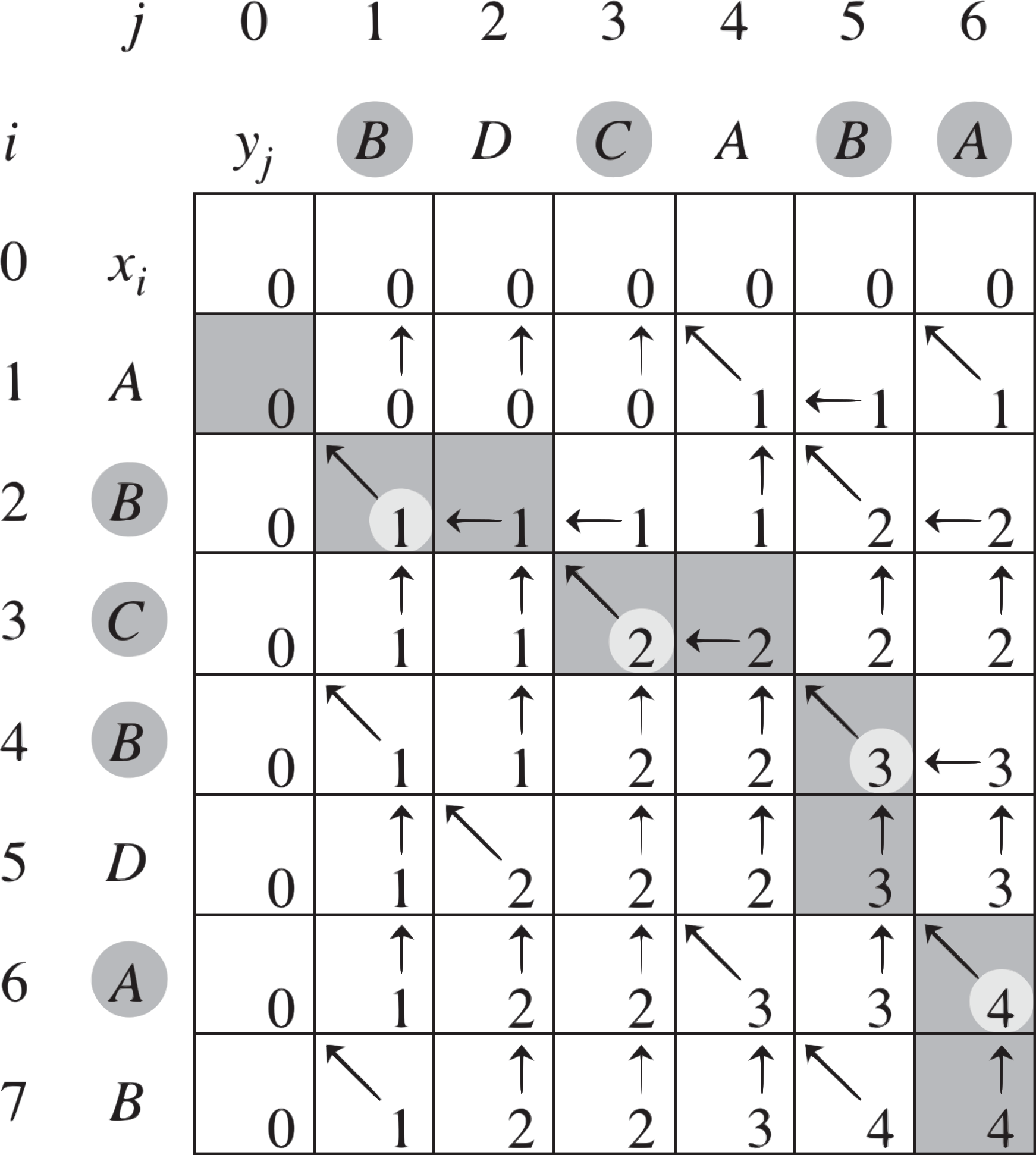
11. Dynamic Programming Slides Notes
    • The Bellman Equation
    • Elements of Dynamic Programming
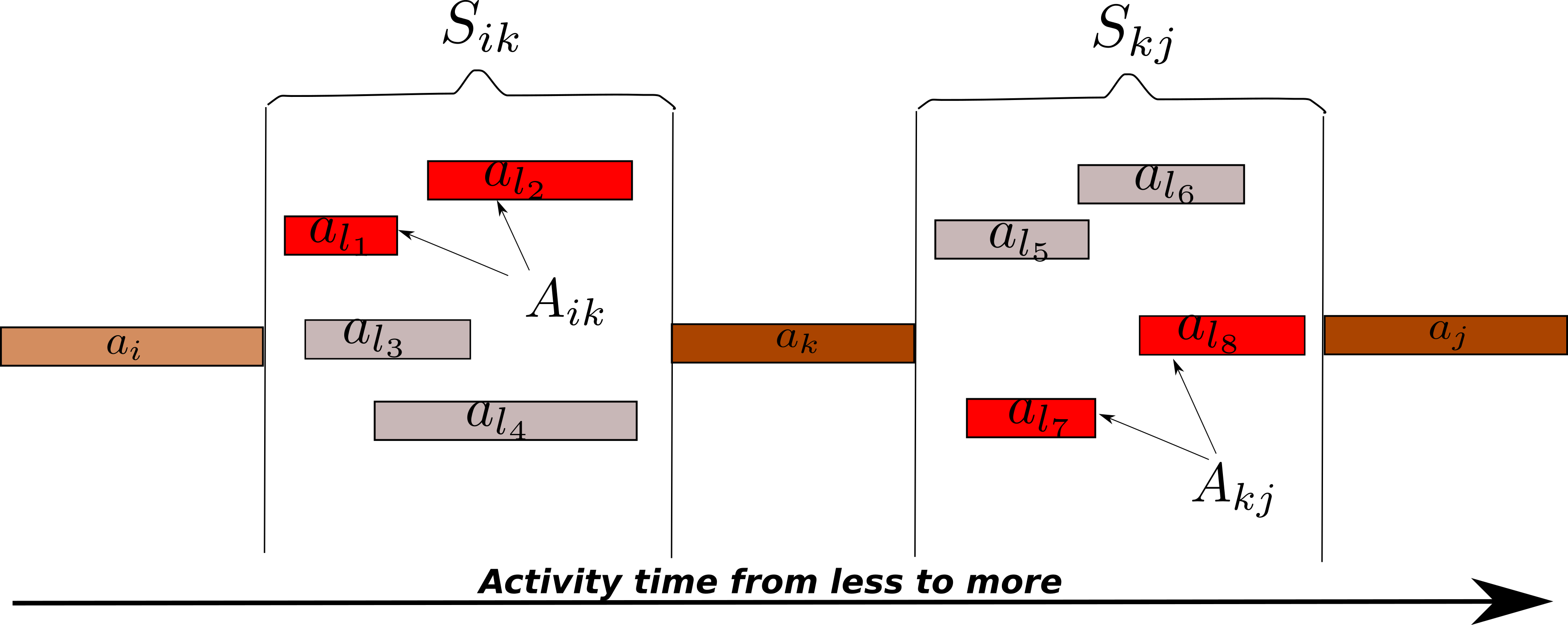
      • Optimal Substructure
      • Overlapping Structures
      • Reconstruction of Sub-problems
      • Common Sub-problems

    

12. Greedy Methods Slides Notes
    • Steps of the Greedy Method
    • Dynamic Programming vs. Greedy Method
    • Examples

    

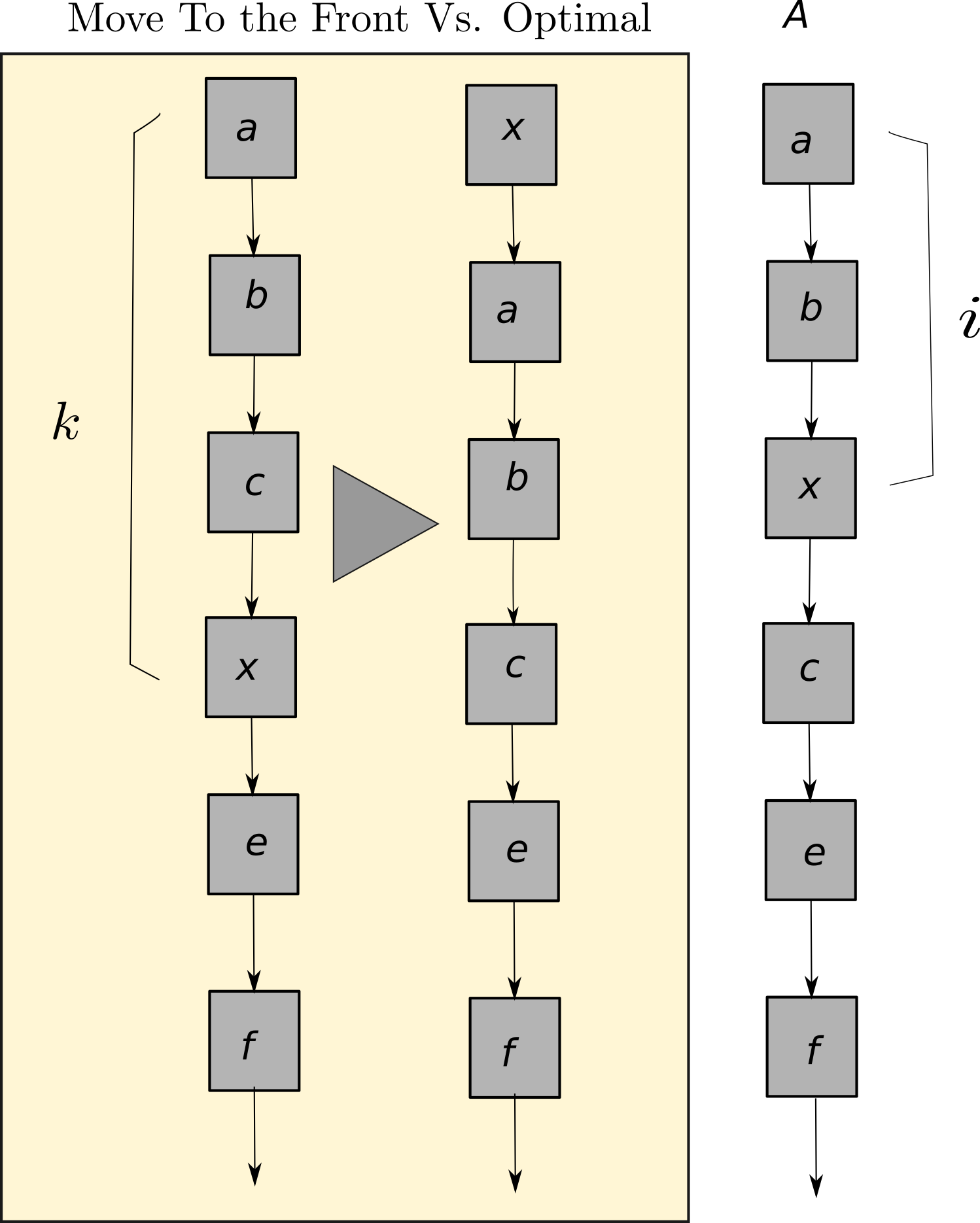
13. Amortized Analysis Slides Notes
    • Introduction
    • Aggregate Method
    • Accounting Method
    • Potential Method
    • Examples

    

14. Skip Lists Slides Notes
    • Dictionaries
    • Improving on dictionary access
    • Skip List and the highway
    • Probability Analysis of Complexity

    

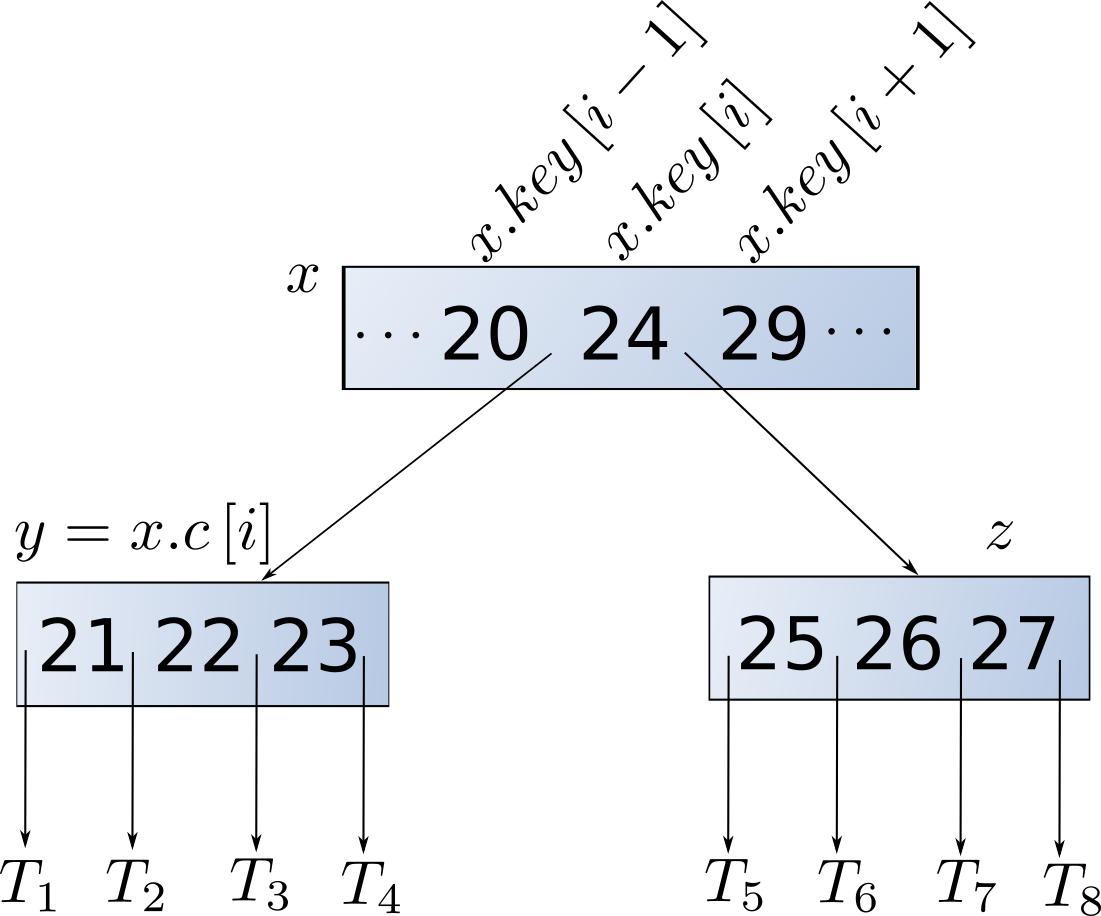
15. B-Trees Slides Notes
    • The Motivation, slow memory hierarchy
    • B-Trees
    • The Height Property
    • Operations

    

16. Fibonacci Heaps Slides Notes
    • Another version of Heaps
    • Definition of Heaps
    • Operations
    • Amortized Analysis

    

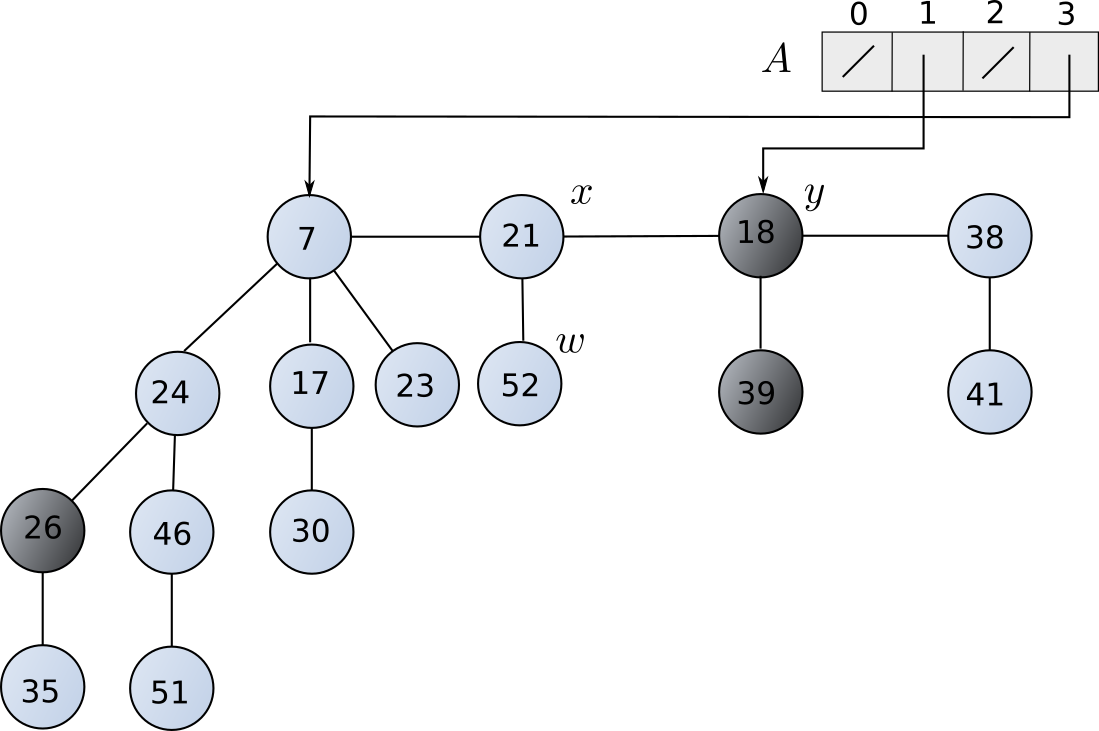
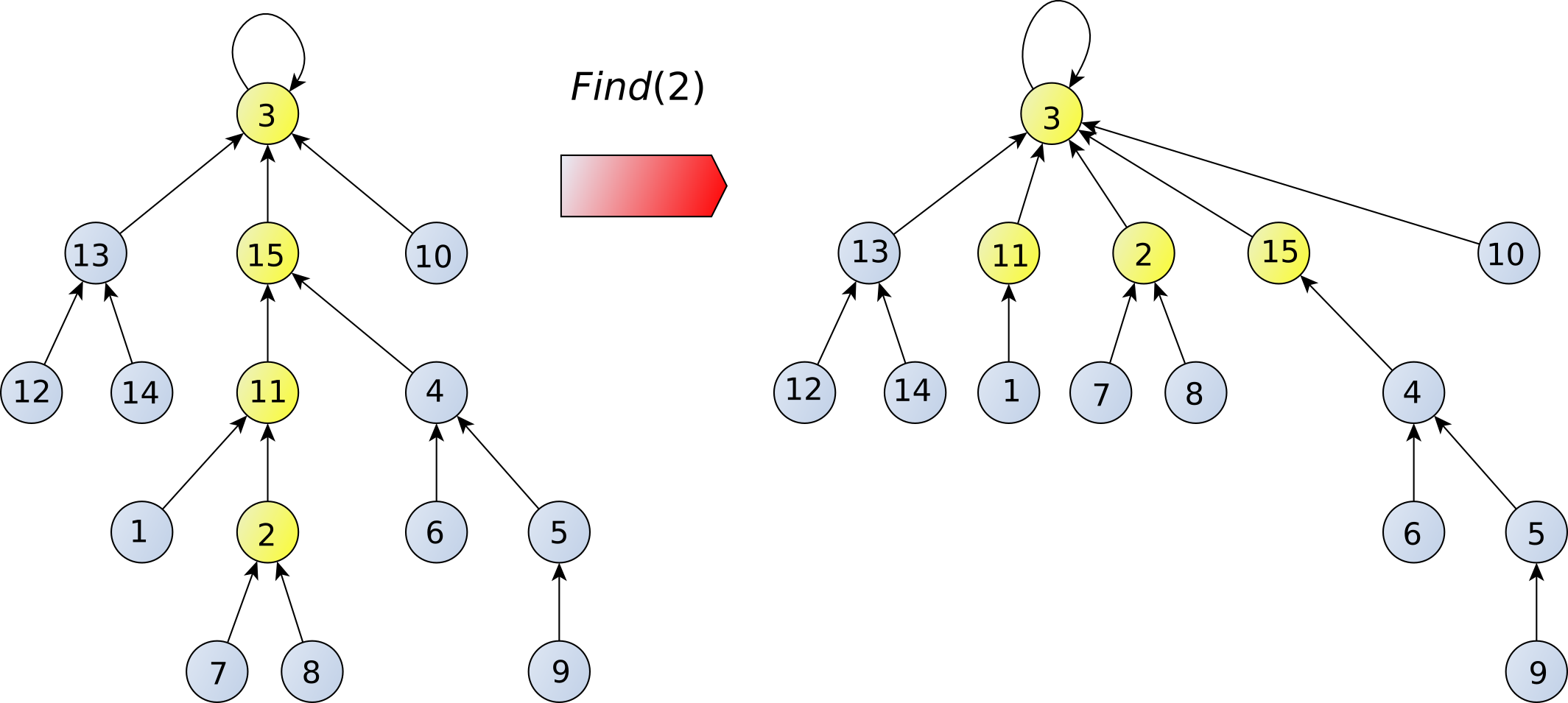
17. Disjoint Set Representations Slides Notes
    • Represent Disjoint Sets
    • Two Strategies: Union by Rank and Path Compression
    • The use of the inverse Ackermann function
    • Getting \(O(m\log^* n)\) complexity for all operations

    

18. Graphs Slides Notes
    • Introduction
    • Breadth First Search
    • Depth First Search
    • Applications

    

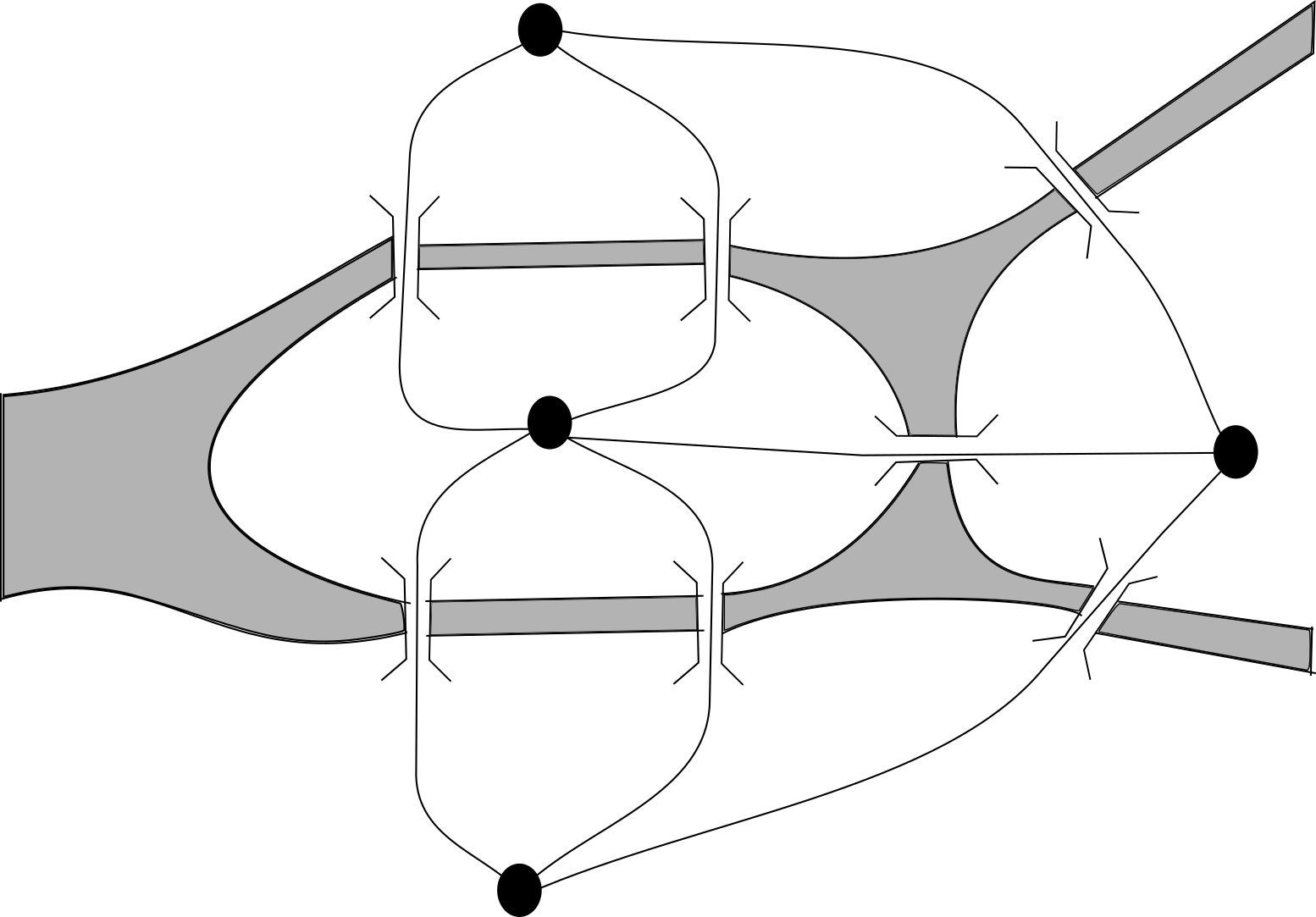
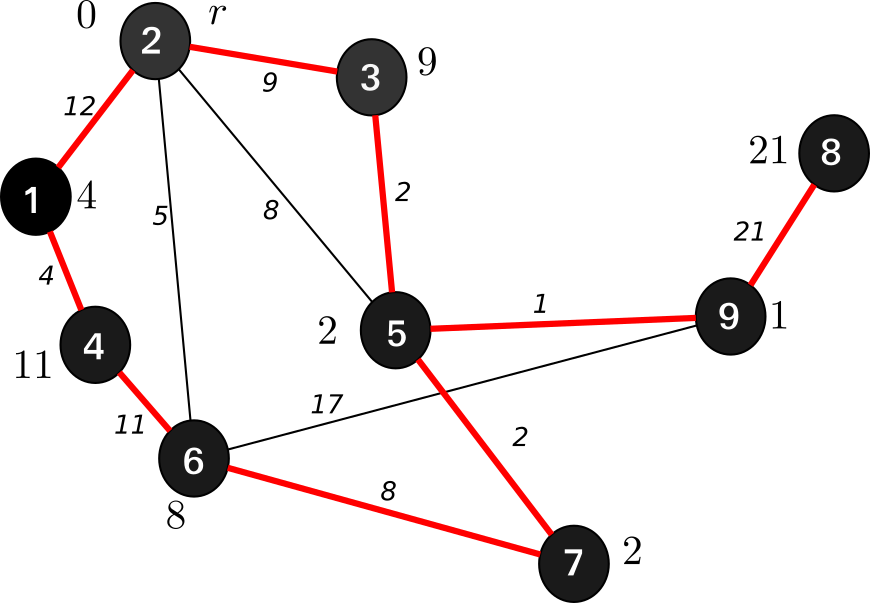
19. Minimum Spanning Trees Slides Notes
    • Introduction
    • The Cut and Light Edge idea
    • The Greedy Algorithms: Kruskal and Prim

    

20. Single Source Shortest Path Slides Notes
    • Introduction
    • The Shortest Path Idea
    • The Dynamic Algorithm, Bellman-Ford
    • A version for Directed Acyclic Graphs
    • A Greedy Algorithm, Dijkstra

    

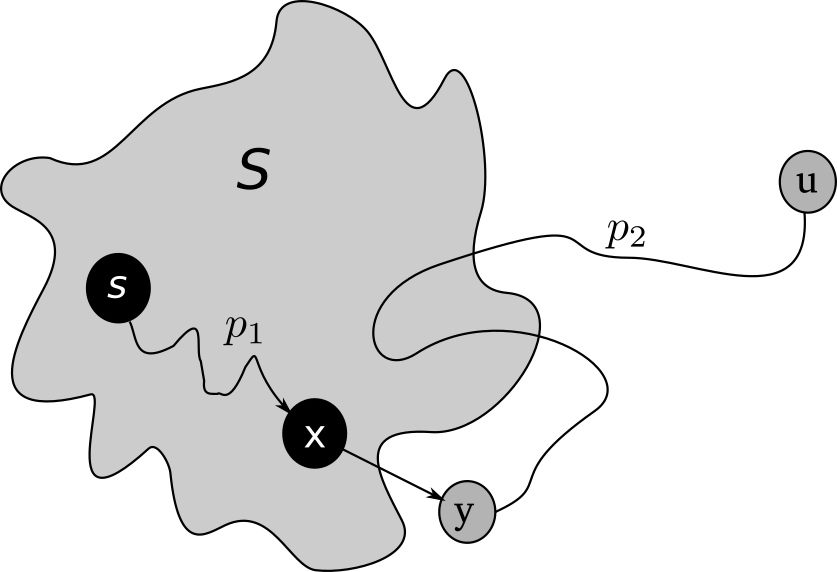
21. All-pairs Shortest Path Slides Notes
    • Using the old algorithms to solve the problem
    • Trying to improve
    • The Floyd-Warshall Algorithm
    • The Johnson’s Algorithm

    

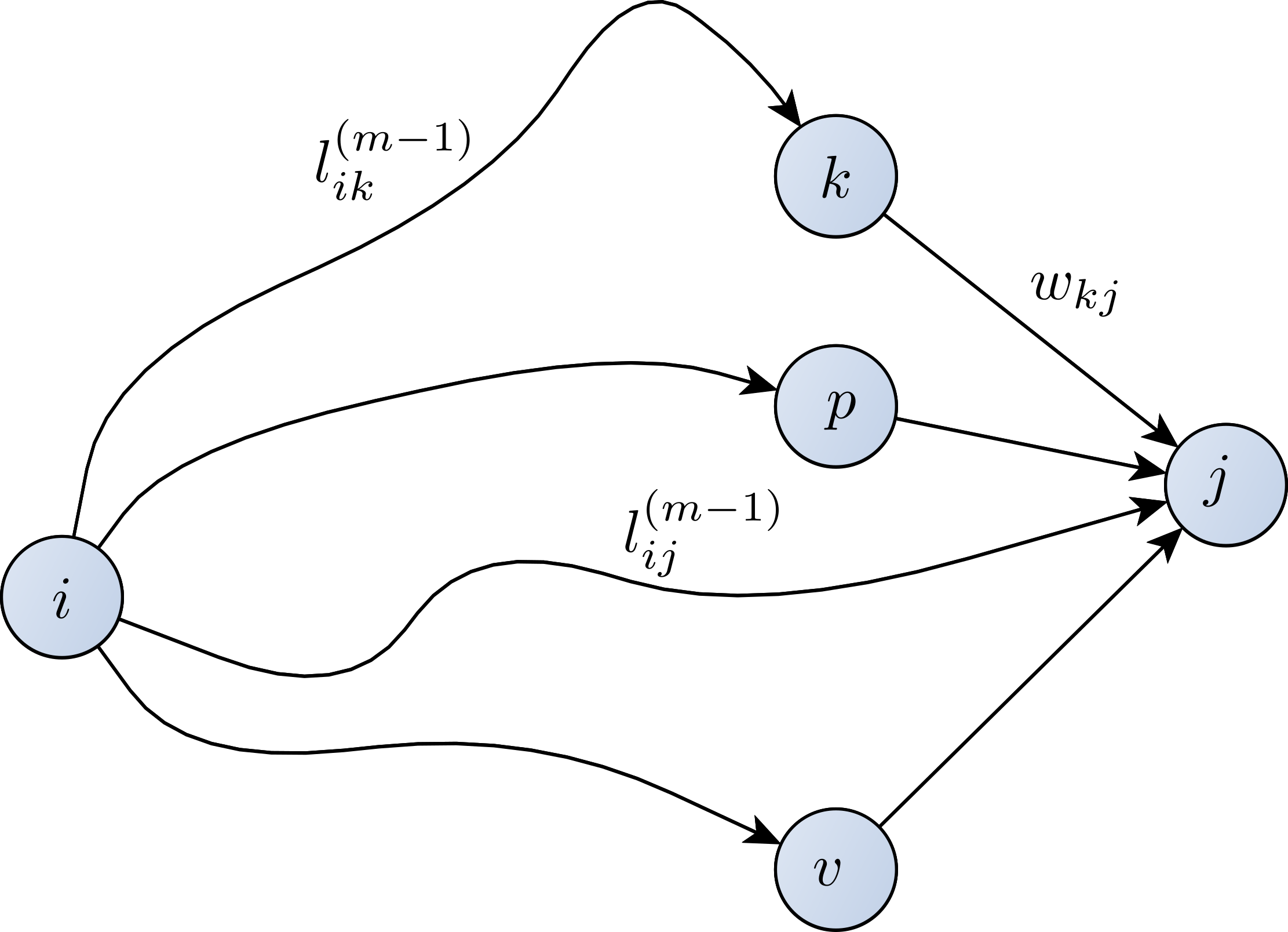
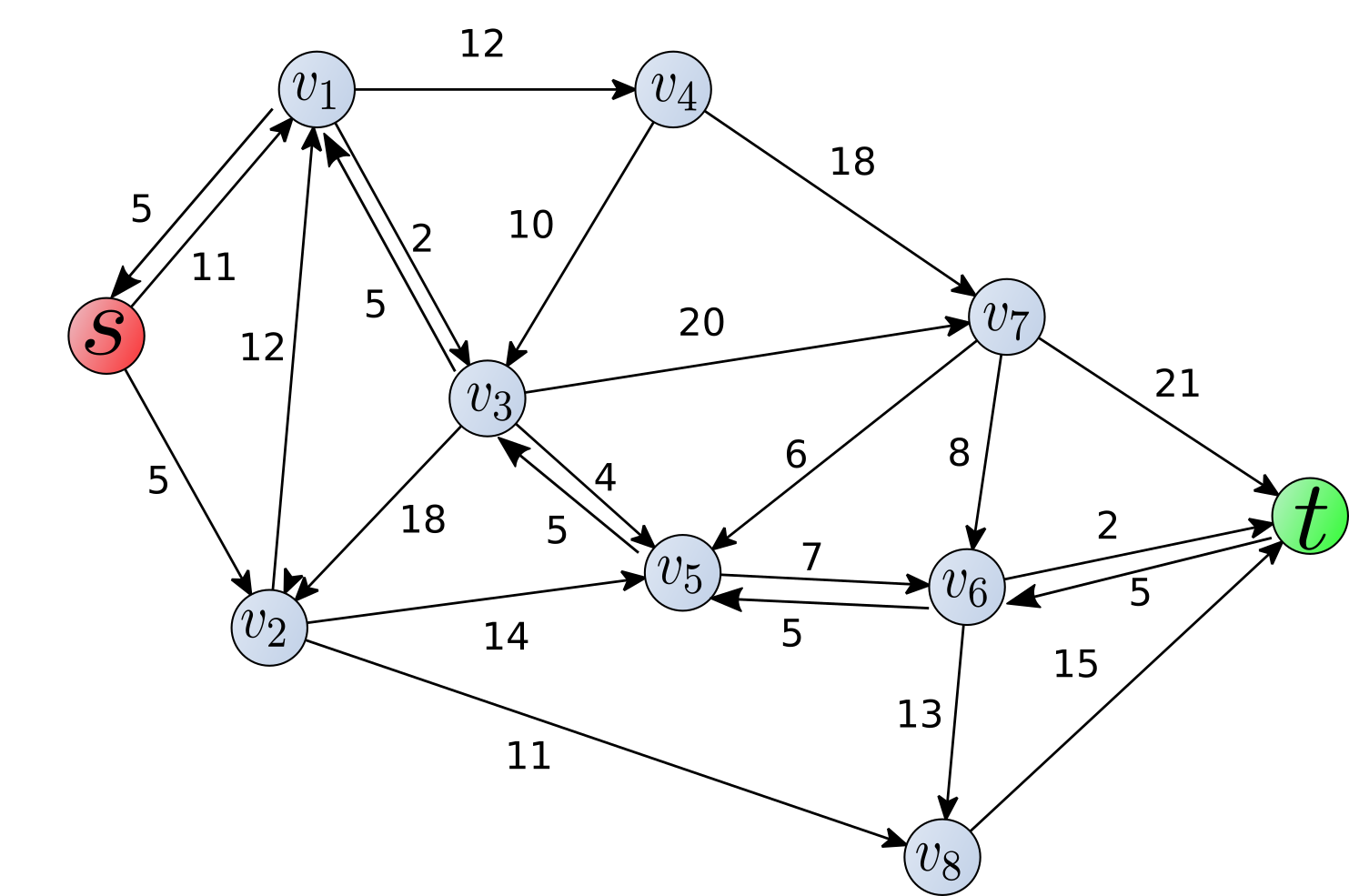
22. Max Flow Slides Notes
    • Flows in Graphs
    • Flow properties
    • The Ford-Fulkerson Mehtod
    • Minimal-cut
    • Improving the Ford-Fulkerson, the Edmond-Karp Algorithm
    • Applications

    

23. Matrix Algorithms Slides Notes
    • Matrix Operations
    • Improving the Matrix Multiplication
    • Solving System of Linear Equations
    • Applications
    \[\left(\begin{array}{cc} 1 & 0\\ \frac{\boldsymbol{v}}{a_{11}} & I_{n-1} \end{array}\right)\left(\begin{array}{cc} a_{11} & \boldsymbol{w}^{T}\\ 0 & \underset{\mbox{Schur Complement}}{\underbrace{A'-\frac{\boldsymbol{v}\boldsymbol{w}^{T}}{a_{11}}}} \end{array}\right)\]
24. Multi-threaded Algorithms Slides Notes
    • Why Multi-threading?
    • Model
    • DAG
    • Performance Measures
    • Parallel Laws
    • Examples
25. String Matching Slides Notes
    • String Matching Basics
    • Naive Algorithms
    • Rabin-Karp
    • Other Algorithms
    • etc
26. Computational Geometry Slides Notes
    • What is Computational Geometry?
    • Representation of Geometries
    • Line-Segment Properties
    • Classic Problems
27. NP-Complete Problems Slides Notes
    • The Polynomial Time
    • Structure of the Polynomial Time
    • Polynomial Time Verification
    • Reducibility
    • NP-Completeness
    • The Basic NP-Problems
28. Dealing with NP-Complete Problems Slides
    • The Dilemma
    • Backtracking
    • Branch and Bound
    • Approximation Algorithms

Geometric Algorithms

1. KD-Trees

2. NNDescent

3. Triangulation

The NP-Problem

1. Approximation Algorithms and Heuristics

Probabilistic Algorithms

1. Skip Lists Slides Notes
   • Why Skip Lists?
   • A Probabilistic Data Structure
   • Definition
   • Bernoulli’s Distribution
     • Search
     • Insertion
     • Deletion

   

2. Locality Sensitive Hashing Slides
   • The Theory Behind it
   • The Practicalities
   • The Shingles
     • k-grams
   • Set representation
   • Min Hash
   • The Signature Matrix
   • Playing the probability game

   

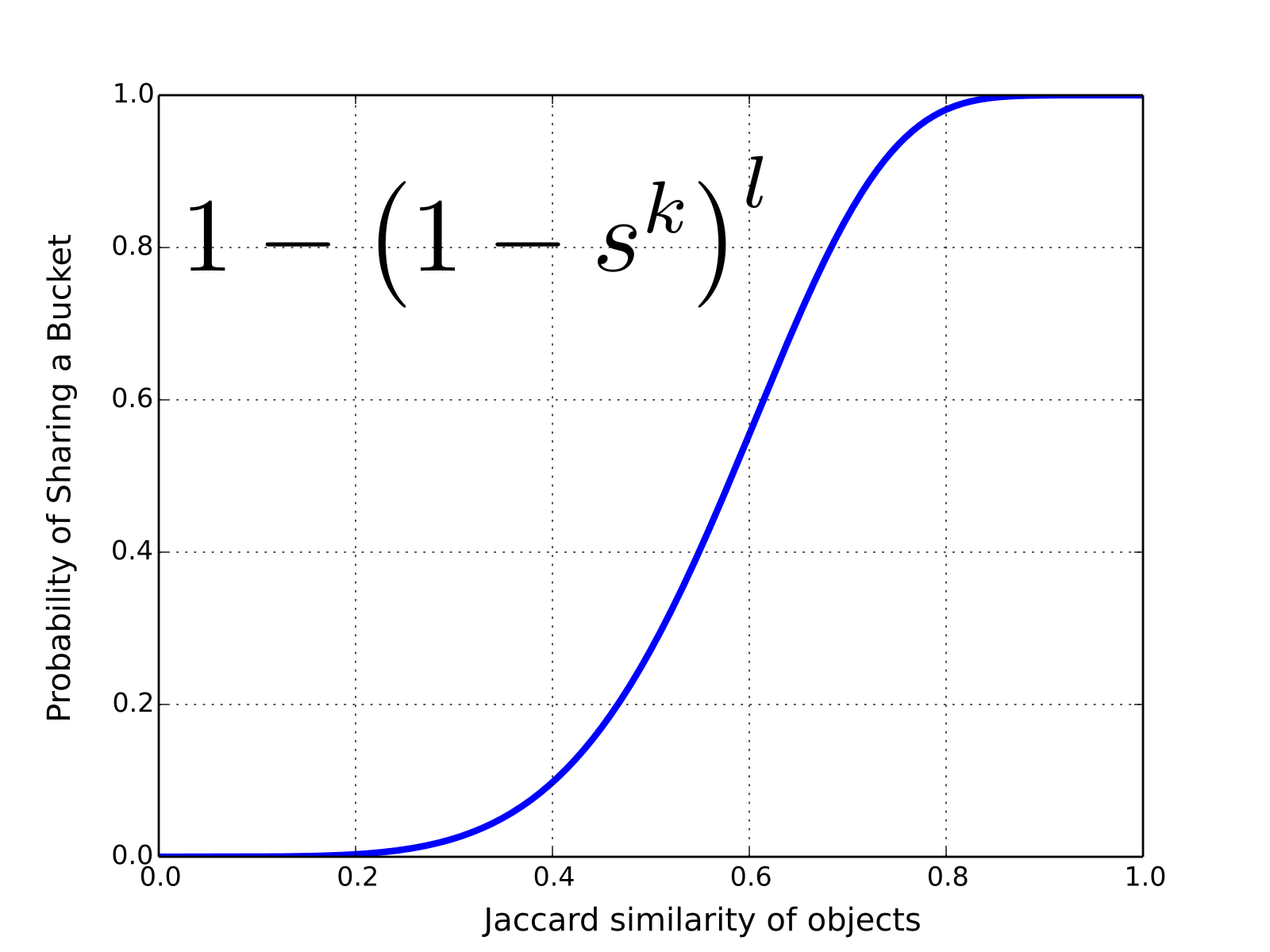
3. Membership Query - Bloom Filter

4. Frequency Count

5. Ranking Q-digest

6. Treaps

7. Distributed Algorithms