These are my attempts to write a series of slides on the many topic of ML.

Introduction slides
- Why Learning?
\[\]
The Basic Ideas of Learning slides
- Some of the basic ideas on Learning
\[\min_{\widehat{f}}R\left(\widehat{f}\right)=\min_{\widehat{f}}E_{\mathcal{X},\mathcal{Y}}\left[\left(\widehat{f}\left(\boldsymbol{x}\right)-y\right)^{2}\vert\boldsymbol{x}\in\mathcal{X}\subseteq\mathbb{R}^{d},y\in\mathcal{Y}\subseteq\mathbb{R}\right]\]
Linear Models slides
- A basic introduction to Linear models
- Some Basic ideas on regularization
- Interludes with Linear Algebra and Calculus
\[g\left(\boldsymbol{\boldsymbol{x}}\right)=\boldsymbol{W^{T}\boldsymbol{x}=\boldsymbol{T}^{T}\left(\boldsymbol{X}^{+}\right)^{T}\boldsymbol{x}}\]
Regularization slides
- A deeper study in the field of regularization
\[C_{h}=\left(A^{T}A+h^{2}I\right)^{-1}A^{T}\]
Batch and Stochastic Gradient Descent slides
- Batch Gradient Descent
- Accelerating Gradient Descent
- Stochastic Gradient Descent
- Minbatch
- Regret in Machine Learning
- AdaGrad
- ADAM
\[\boldsymbol{w}_{n}=\boldsymbol{w}_{n-1}+\mu_{n}\boldsymbol{x}_{n}\left(\boldsymbol{x}_{n}^{T}\boldsymbol{w}_{n-1}-y_{n}\right)\]
Logistic Regression slides
- Interlude with Generative vs Discriminative models
- The Logistic Regression model
- Accelerating the logistic regression
\[\mathcal{L}\left(\boldsymbol{w}\right)=\sum_{i=1}^{N}\left\{ y_{i}\boldsymbol{w}^{T}\boldsymbol{x}_{i}-\log\left(1+\exp\left\{ \boldsymbol{w}^{T}\boldsymbol{x}_{i}\right\} \right)\right\}\]
Introduction to Bayes Classification slides
- Naive Bayes
- Discriminative Functions
\[\ln L\left(\omega_{i}\right)=-\frac{n}{2}\ln\left|\Sigma_{i}\right|-\frac{1}{2}\left[\sum_{j=1}^{n}\left(\boldsymbol{x_{j}}-\boldsymbol{\mu_{i}}\right)^{T}\Sigma_{i}^{-1}\left(\boldsymbol{x_{j}}-\boldsymbol{\mu_{i}}\right)\right]+c_{2}\]
Maximum a Posteriori Methods
- Going beyond Maximum Likelihood
- The General Case
- How can be used in Bayesian Learning?
\[p\left(\boldsymbol{w},\sigma^{2}\vert\boldsymbol{y},\tau\right)\propto p\left(\boldsymbol{y}\vert\boldsymbol{w},\sigma^{2}\right)p\left(\boldsymbol{w}\vert\tau\right)p\left(\sigma^{2}\right)\]
EM Algorithm slides
- A classic example of the use of the MAP
- Its use in clustering
\[Q\left(\Theta\vert\Theta^{g}\right)=\sum_{\boldsymbol{y}\in\mathcal{Y}}\sum_{i=1}^{N}\log\left[\alpha_{y_{i}}p_{y_{i}}\left(x_{i}\vert\theta_{y_{i}}\right)\right]\prod_{j=1}^{N}p\left(y_{j}\vert x_{j},\Theta^{g}\right)\]
Feature Selection slides
- Introduction to the curse of dimensionality
- Normalization the classic methods
- Data imputation using EM and Matrix Completion
- Methods for Subset Selection
- Shrinkage methods, the classic LASSO
\[\widehat{\boldsymbol{w}}^{LASSO}=\arg\min_{\boldsymbol{w}}\left\{ \sum_{i=1}^{N}\left(y_{i}-\boldsymbol{x}^{T}\boldsymbol{w}\right)^{2}+\lambda\sum_{i=1}^{d}\left|w_{i}\right|^{q}\right\} \mbox{ with }q\geq0\]
Feature Generation slides
- Introduction
- Fisher Linear Discriminant
- Principal Component Analysis
- Singular Value Decomposition
\[L\left(\boldsymbol{u}_{2},\lambda_{1},\lambda_{2}\right)=\boldsymbol{u}_{2}^{T}S\boldsymbol{u}_{2}-\lambda_{1}\left(\boldsymbol{u}_{2}^{T}\boldsymbol{u}_{2}-1\right)-\lambda_{2}\left(\boldsymbol{u}_{2}^{T}\boldsymbol{u}_{1}-0\right)\]
Measures of Accuracy slides
- The alpha beta errors
- The Confusion Matrix
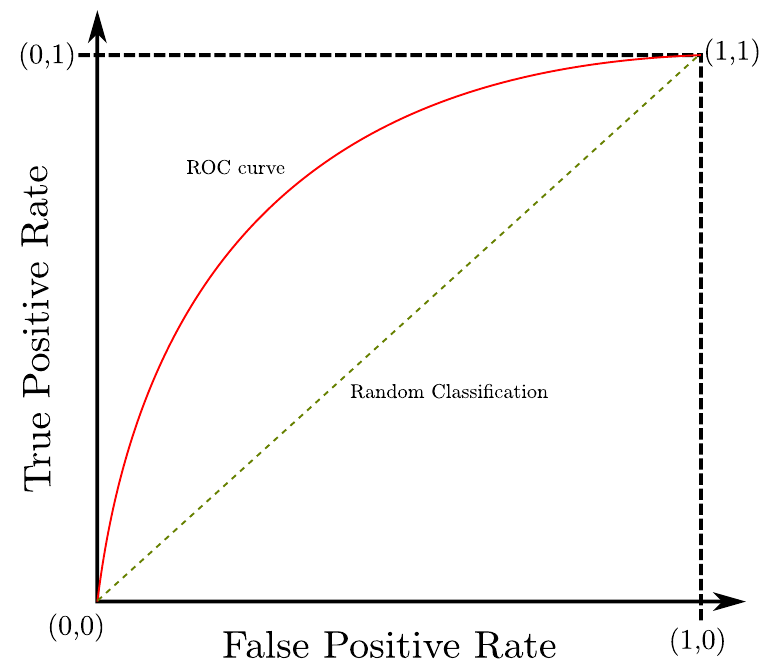
- The ROC curve
Hidden Markov Models slides
- Another classic example of the use of Dynamic Programming and EM
- The Three Problems
\[\hat{L}\left(\lambda,\lambda^{n}\right)= \hat{Q}\left(\lambda,\lambda^{n}\right)-\lambda_{\pi}\left(\sum_{i=1}^{N}\pi_{i}-1\right)-\sum_{i=1}^{N}\lambda_{a_{i}}\left(\sum_{j=1}^{N}a_{ij}-1\right)-\sum_{i=1}^{N}\lambda_{b_{i}}\left(\sum_{k=1}^{M}b_{i}\left(k\right)-1\right)\]
Support Vector Machines slides
- The idea of margins
- Using the dual solution
- The kernel trick
- The soft margins
\[Q(\alpha)={\displaystyle \sum_{i=1}^{N}\alpha_{i}-\frac{1}{2}\sum_{i=1}^{N}\sum_{j=1}^{N}\alpha_{i}\alpha_{j}d_{i}d_{j}\boldsymbol{x}_{j}^{T}\boldsymbol{x}_{i}}\]
The Perceptron slides
- The first discrete neural network
- The Idea of Learning
\[y\left(i\right)=v\left(i\right)=\sum_{i=1}^{m}w_{k}\left(i\right)x_{k}\left(i\right)\]
Multilayer Perceptron slides
- The Xor Problem
- The Hidden Layer
- Backpropagation for the new architecture
- Heuristic to improve the performance
\[\triangle w_{kj}=\eta\delta_{k}y_{j}=\eta\left(t_{k}-z_{k}\right)f'\left(net_{k}\right)y_{j}\]
The Universal Representation Theorem slides
- Cybenko Theorem
\[G\left(\boldsymbol{x}\right)=\sum_{j=1}^{N}\alpha_{j}f\left(\boldsymbol{w}^{T}\boldsymbol{x}+\theta_{j}\right)\]
Convolutional Networks slides
- Introduction to the image locality problem
- How convolutions can solve this problems
- Backpropagation on the CNN
\[\left(f*g\right)\left[x,y\right]=\sum_{k=-n}^{n}\sum_{l=-n}^{n}f\left(k,l\right)g\left(x-k,y-l\right)\]
Regression and Classification Trees slides
- Using decision trees for Regression
- The Classification Tree
- Entropy to build the Classification Tree
\[\Delta I\left(t\right)=I\left(t\right)-\frac{N_{tY}}{N_{t}}I\left(t_{Y}\right)-\frac{N_{tN}}{N_{t}}I\left(t_{N}\right)\]
Vapnik-Chervonenkis Dimensions slides
- Can we learn?
- The Shattering of the space
- The Inequality
- How to measure the power of a classifier
\[E_{in}\left(g\right)<E_{out}\left(g\right)+\sqrt{\frac{2k}{N}\ln\frac{eN}{k}}+\sqrt{\frac{1}{2N}\ln\frac{1}{\delta}}\]
Combining Models and Boosting slides
- Bagging
- Mixture of Experts
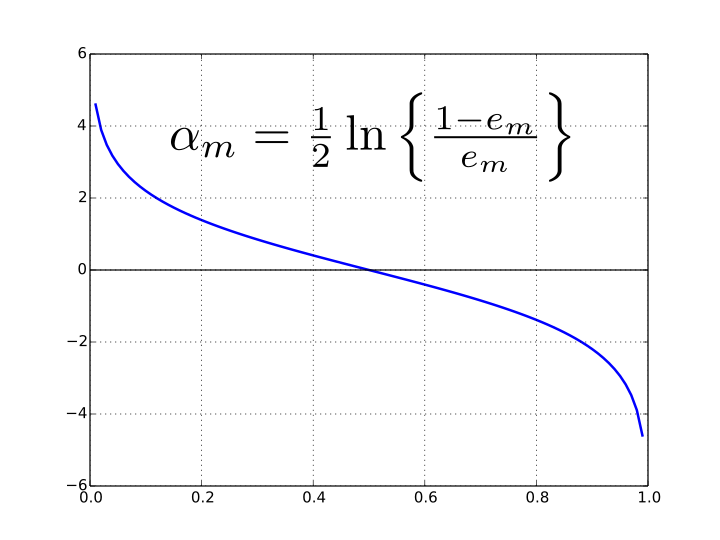
- AdaBoosting
Boosting Trees, XBoost and Random Forrest slides
- Using Boosting in Trees
- Random Forrest
- Taylor approximation for Boosting Trees
\[\mathcal{L}^{\left(t\right)}\simeq\sum_{i=1}^{N}\left[g_{i}f_{t}\left(\boldsymbol{x}_{i}\right)+\frac{1}{2}h_{i}f_{t}^{2}\left(\boldsymbol{x}_{i}\right)\right]+\Omega\left(f_{t}\right)\]
Introduction to Clustering slides
- The idea of finding patterns in the data
- The need for a similarity for the data
- The different features
K-Means, K-Center and K-Meoids slides
- The NP-Problem of Clustering
- Using Cost functions for finding Clusters
- Using Approximation Algorithms for Clustering
- Beyond the metric space
\[\sum_{k=1}^{N}\sum_{i:\boldsymbol{x}_{i}\in C_{k}}\left\Vert \boldsymbol{x}_{i}-\boldsymbol{\mu}_{k}\right\Vert ^{2}=\sum_{k=1}^{N}\sum_{i:\boldsymbol{x}_{i}\in C_{k}}\left(\boldsymbol{x}_{i}-\boldsymbol{\mu}_{k}\right)^{T}\left(\boldsymbol{x}_{i}-\boldsymbol{\mu}_{k}\right)\]
Hierarchical Clustering and Clustering for Large Data Sets slides
- Introduction
- The idea of nesting
- Bottom-Up Strategy
- Top-Down Strategy
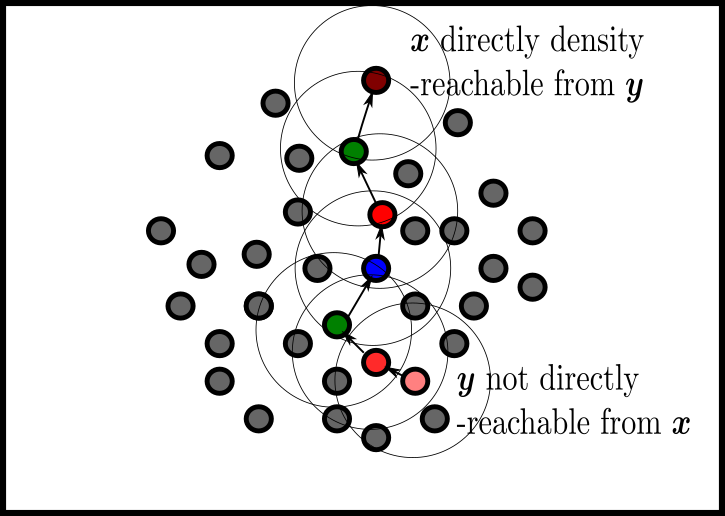
- Large Data Set Clustering: CURE and DBASE
Cluster Validity slides
- An Introduction to cluster validity
\[W\left(\theta\right)=P\left(q\in\overline{D}_{\rho}\vert\theta\in\Theta_{1}\right)\]
Associative Rules slides
- From the era of warehouses, finding frequent rules in databases
Locality Sensitive Hashing slides
- Hashing to find similar elements
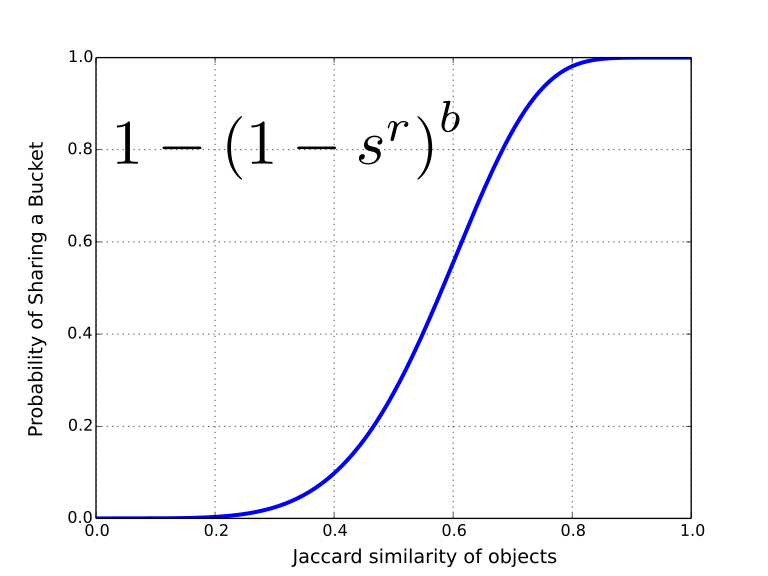
Page Rank slides
- The Web as a Stochastic Matrix
- The Ranking as probabilistic vector
- The Power Method for finding the vector distribution
\[A=\beta M+(1-\beta)\frac{1}{n}\mathbf{e}\cdot\mathbf{e^{T}}\]
Semi-supervised Learning slides
- The Basic of Semi-supervised Learning
- Using it on document labeling
\[P\left(\boldsymbol{x}_{i}\vert\theta\right)=P\left(\left|\boldsymbol{x}_{i}\right|\right)\sum_{j\in\left\{ 1,2,...,M\right\} }P\left(c_{j}\vert\theta\right)\prod_{w_{t}\in\mathfrak{X}}P\left(w_{t}\vert c_{j},\theta\right)^{x_{it}}\]

Book Chapters on Machine Learning

Here the book chapters based on these slides

An Introduction to Learning
Linear Models

UNDER CONSTRUCTION