Introduction to Deep Learning

Here, we have some of my attempts to interpret the field of Deep Learning

1. Introduction Slides
   • Introduction
   • The Neural Architecture
   • Types of activation functions
   • McCulloch-Pitts model
   • Vanishing Gradient

   

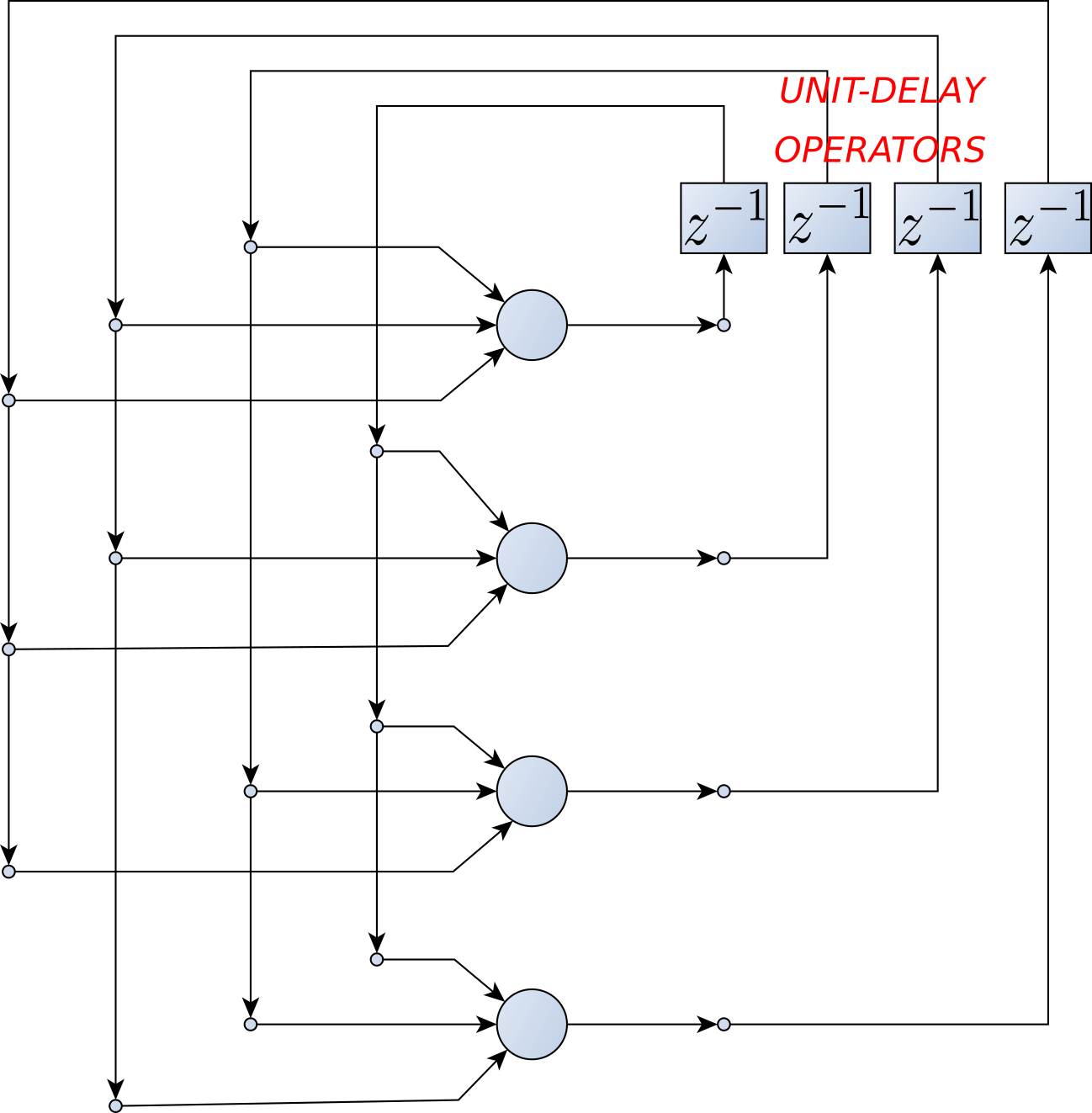
2. Neural Networks as graphs
   • Examples
   • Architectures
   • Design of neural networks
   • Representing knowledge on a Neural Network

   

3. Learning Slides
   • Introduction
   • Error correcting learning
   • Memory based Learning
   • Hebbian Learning
   • Competitive Learning
   • Boltzmann Learning
   \[f\left(x_{t}\right)=\begin{cases} w_{t}\times\sigma\left(x_{t}\right) & \mbox{ if }x_{t}>t\mbox{ and }w_{t+1}=\alpha w_{t}\mbox{ with } \alpha>1\\ w_{t}\times\sigma\left(x_{t}\right) & \mbox{ if }x_{t}>t\mbox{ and }w_{t+1}=\alpha w_{t}\mbox{ with } \alpha<1 \end{cases}\]
4. Perceptron Slides
   • History and the beginning as PDE
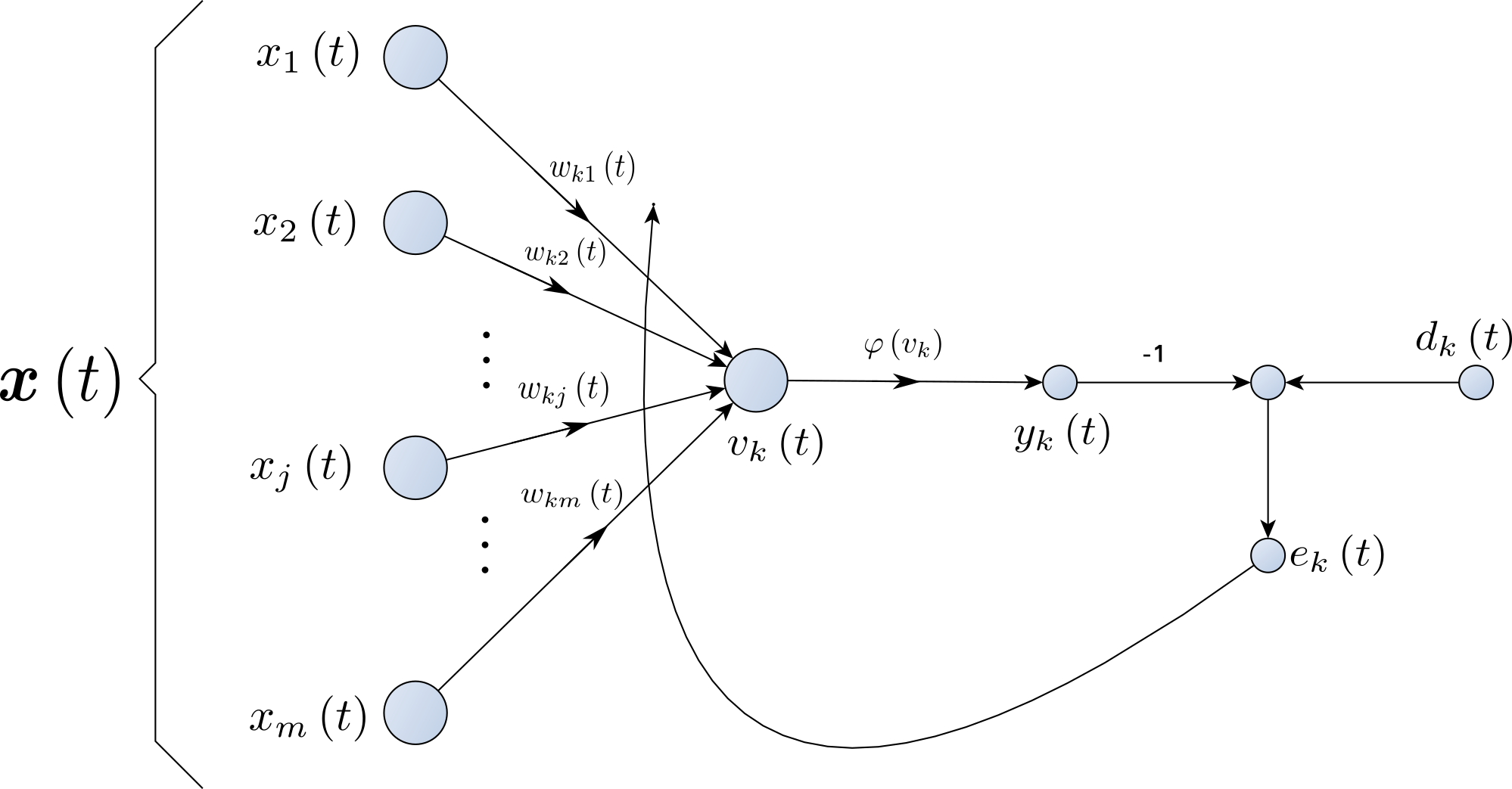
   • Adaptive Filtering
   • Rosenblatt’s algorithm

   

5. Multilayer Perceptron Slides
   • Solving the XOR problem
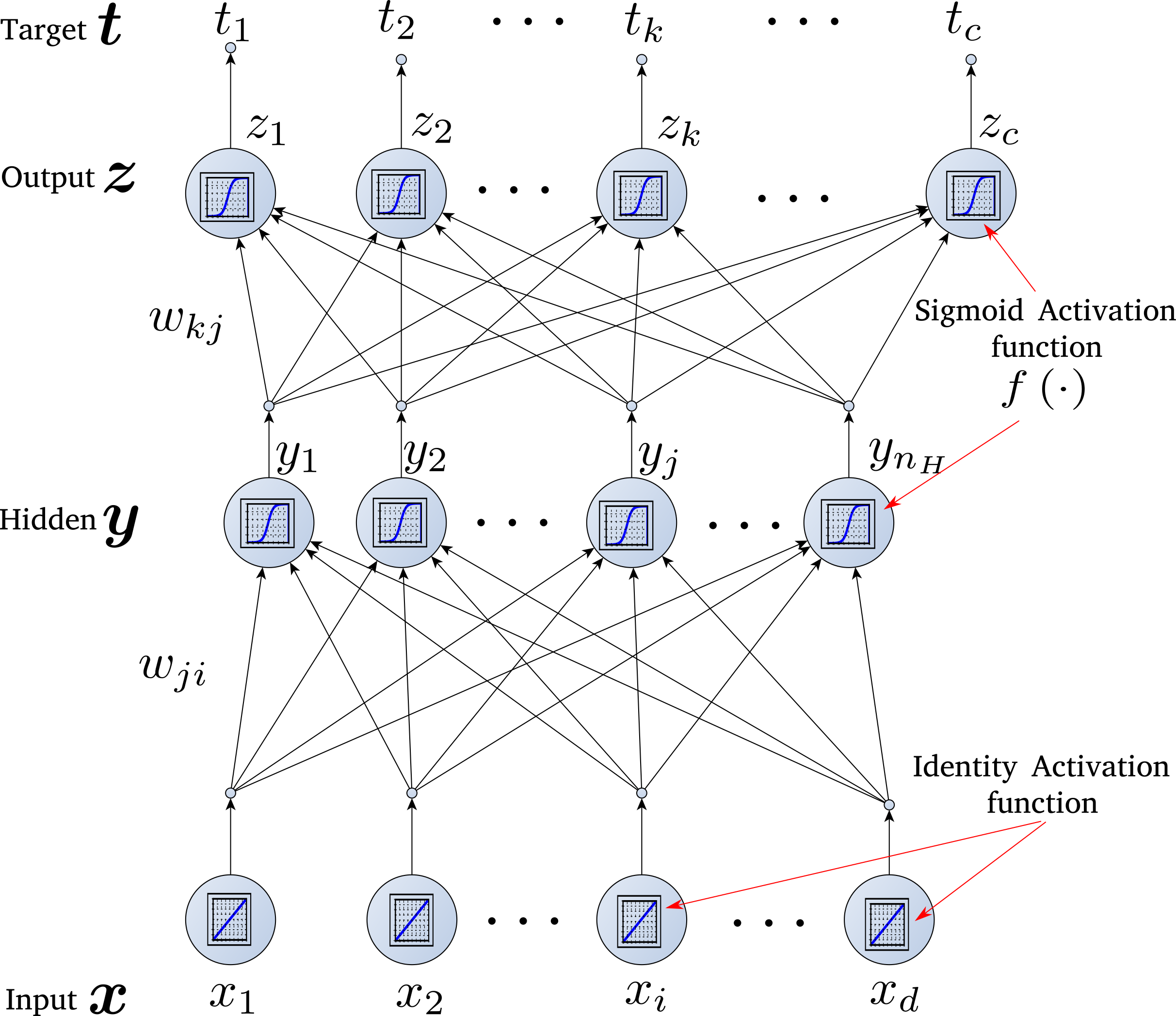
   • The basic architecture
   • Backpropagation
   • Matrix form of the backpropagation
   • The Universal Approximation Theorem

   

6. Deep Forward Networks Slides
   • The problem with shallow architectures - lack of expressiveness
   • From simple features to complex ones
   • Component of Deep Forward Architectures
   • The Problems with the Gradient in Deeper Architectures
   • RELU a possible solution
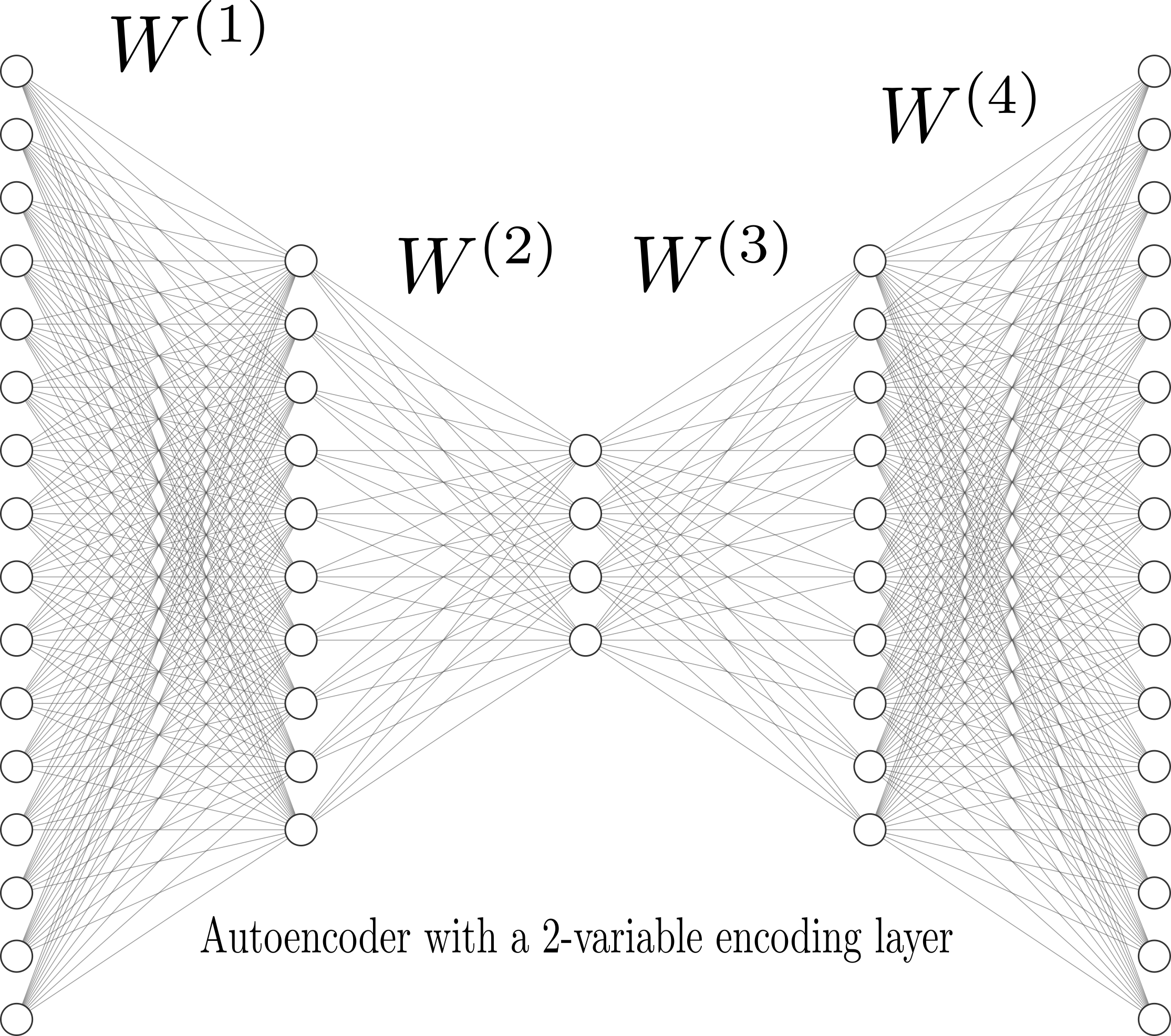
   • Examples of Deep Architectures: Generative, Residual, Autoencoders, Boltzmann Machines, etc

   

7. The idea of Back-propagation and Automatic Differentiation Slides
   • Derivation of Network Functions
   • Function Composition
   • The Rule Chain AKA Backpropagation
   • Advantages of Automatic Differentiation
   • Forward and Reverse Method
   • Proving the Reverse Method
   • Basic Implementation of Automatic Differentiation
   \[A_{i}\equiv\left[\begin{array}{ccccccc} 1 & 0 & \ldots & 0 & \ldots & \ldots & 0\\ 0 & 1 & \ldots & 0 & \ldots & \ldots & 0\\ \vdots & \vdots & \ddots & \vdots & \ldots & \ldots\\ 0 & 0 & \ldots & 1 & \ldots & \ldots & 0\\ c_{i1-n} & c_{i2-n} & \ldots & c_{ii-n} & \ldots & \ldots & 0\\ 0 & 0 & \ldots & 0 & 1 & \ldots & 0\\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots\\ 0 & 0 & \ldots & \ldots & \ldots & \ldots & 1 \end{array}\right]\in\mathbb{R}^{\left(n+l\right)\times\left(n+l\right)}\]
8. Stochastic Gradient Descent Slides
   • Review Gradient Descent
   • The problem with Large Data sets
   • Convergence Rate
   • Accelerate the Gradient Descent: Nesterov
   • Robbins-Monro idea
   • SGB vs BGD
   • The Minbatch
   • Least-Mean Squares Adaptive
   • AdaGrad
   • ADAM
   \[\sum_{k=1}^{t}\frac{\widehat{m}_{k}}{\left(\sqrt{\widehat{v}_{k}}\right)}=\sum_{k=1}^{t}\frac{\frac{m_{k}}{\left(1-\beta_{1}^{k}\right)}}{\left(\sqrt{\frac{v_{k}}{\left(1-\beta_{2}^{k}\right)}}\right)}=\sum_{k=1}^{t}\frac{\left(1-\beta_{2}^{k}\right)^{\frac{1}{2}}}{\left(1-\beta_{1}^{k}\right)}\times\frac{m_{k}}{\sqrt{v_{k}}}\]
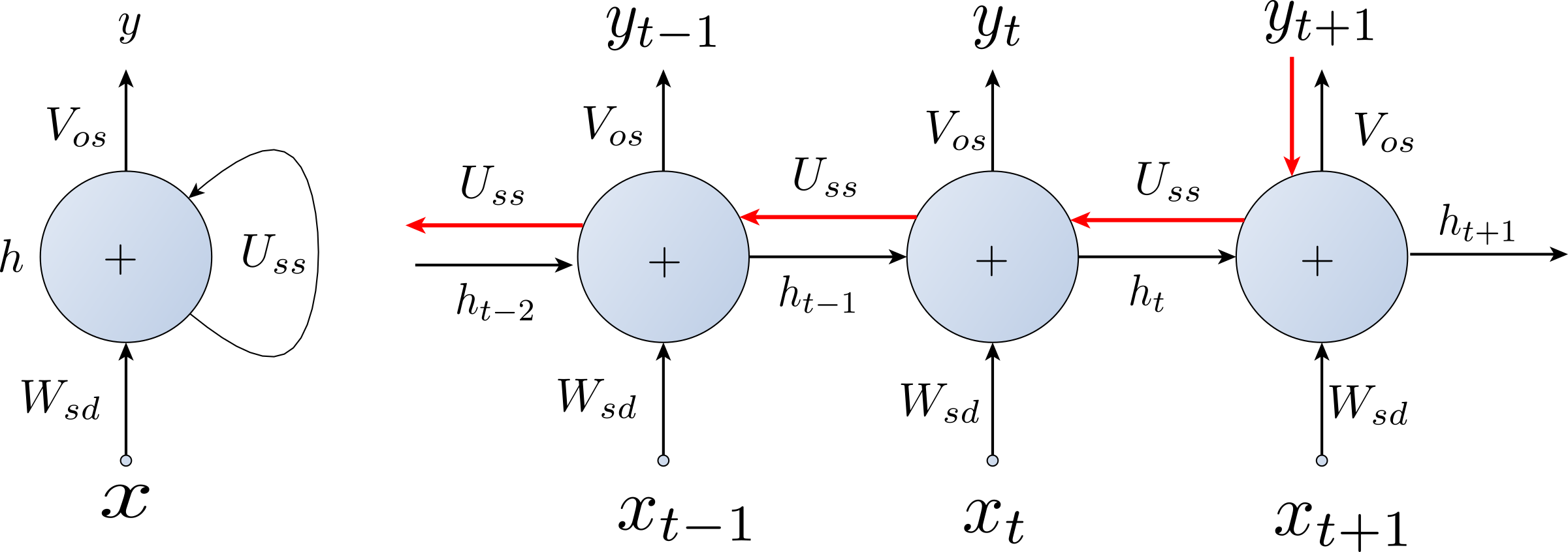
9. Introduction to Recurrent Neural Networks Slides
   • Vanilla RNN
   • The Training Problem
   • Backpropagation Though Time (BPTT)
   • Dealing with the problem LSTM and GRU
   • Can we avoid the BPTT?

   

10. Regularization in Deep Neural Networks Slides
    • Bias-Variance Dilemma
    • The problem of overfitting
    • Methods of regularization in Deep Neural Networks
      • Dropout
      • Random Dropout Probability
      • Batch Normalization
    \[y_{i}=BN_{\gamma,\beta}\left(\boldsymbol{x}_{i}\right)\]
11. Convolutional Networks Slides
    • The problem of the translation on images
    • The need of locality
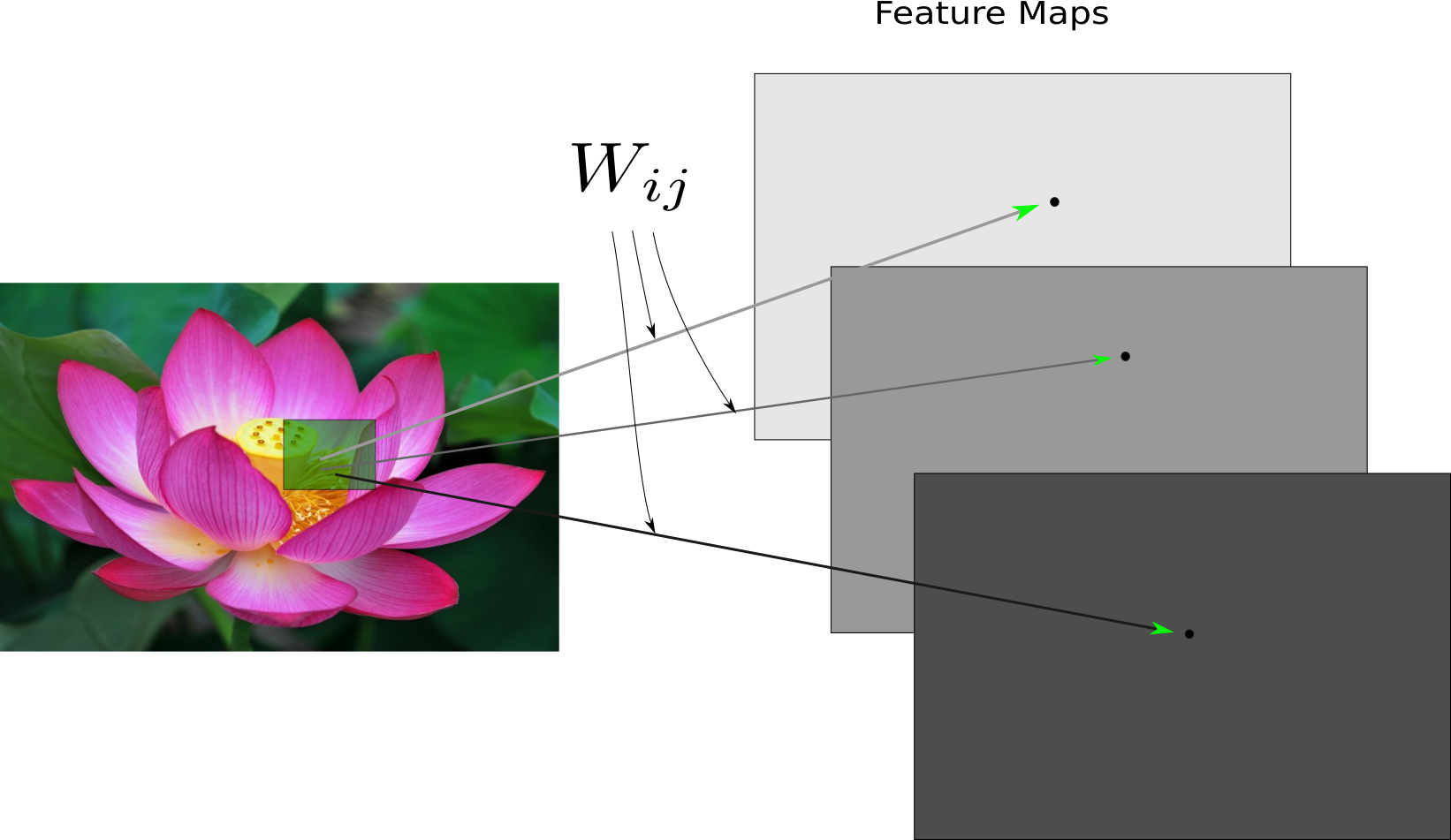
    • The Convolutional Operator
    • Convolutional Networks
    • Layers in Convolutional Networks
    • An Example

    

12. Loss Functions Slides
    • The Loss Functions
    • Hilbert Spaces
    • Reproducibility
    • The Quadratic Loss
    • The problem with it
    • The Logistic and 0-1 Loss
    • Alternatives
    • Beyond Convex Loss Functions
    • Conclusions
    \[L=-\sum_{i=1}^{C}z_{i}\log\left(f\left(y_{i}\right)\right)=-log\left(\frac{\exp\left\{ y_{p}\right\} }{\sum_{j=1}^{C}\exp\left\{ y_{p}\right\} }\right)\]

13. Boltzmann Machines

    \[\]

14. Autoencoders

    \[\]

15. Evaluation of Deep Neural Networks

    \[\]

16. Generative Adversarial Networks

    \[\]

17. Transfer Learning

    \[\]

18. Deep Residual Networks

    \[\]

19. Second Order Methods

    \[\]

20. Partial Differential Equations in Deep Learning

    \[\]

UNDER CONSTRUCTION