Applied Mathematics and the Problem of Context
Recently, I got into a discussion with a person from telecomunications on the subject of context. Context? Yes, the bothersome problem on the subject of Applied Math. Wait a minute, you will say What? I know is quite annoying to ask about context. Let me explain, what happens in education is that you were taught that math was basically an immobile object… always true and eternal… which is true if you talk about the purist world of concepts beyond physical laws and constraints. Yes the parallelogram rule is always true, but as Goedel proved long ago in his theorem [1]:
-
Theorem of Incompleteness
Any consistent formal system \(F\) within which a certain amount of elementary arithmetic can be carried out is incomplete; i.e., there are statements of the language of \(F\) which can neither be proved nor disproved in \(F\).
But you can say, but there is a proof of it? What are you talking about? Then, I say, yes!! You are correct, if you are in a Euclidean Space. The ball falls… you have a context… your space is a simple hyperplane no singularities or deformations on it. It is the infamous context which you cannot prove or disprove that your really live on it. Then, you finally understand my comment about the concept space of ideas. There everything is fine pure and perfect! But in applied math, context is everything and important it is. For example, not for nothing, the count of Buffon went to throw a coin thousand of times over a floor covered with identically shaped tiles. After all, the math for probability was not usable, if it was not able to describe the results of such experiments. Thus, we propose the following baseline:
-
Remark
A problem in the real world forces a set of variables \(X\) in a non-deterministic and non-smooth way in a series of non-deterministic and non-smooth set operators \(D_f\).
Given that our system of sensors is limited, knowing such variables is limited in many ways. Thus, we define a sensor as a function between our smooth variables and the function \(f\in D_f\):
-
Definition (Interface)
A sensor is a interface between a function \(f \in D_f\) and a smooth function \(g \in S_g\):
\[\mathcal{G}:D_{f}\rightarrow S_{g}\]
Here, the smooth function has a small variance making possible to be interpretable. There, an interpretable function can well-possed or ill-possed [2] given that even ill-possed functions cab be regularized increasing their interpretability. You can think of such functions as smoothing over a high variance mapping.
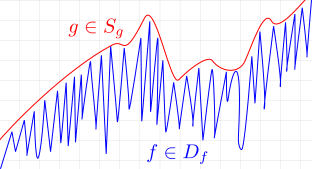
Making possible to say that a sensor will always filter most of the data given the variability of the reality operator which still depends on other variables which could be high variable or not. Basically, the variance of the basic variables are being tamed by the reality operator. Therefore, we have the following definition:
-
Definition (Context):
The context is the interpretation of the data coming from the sensor. Such interpretation is based in a model \(M\), mathematical or not, with a certain bias based in prior knowledge on previous contexts.
Thus, What kind of context are we getting at the end of the pipeline? Given that we are in the realm of the possible, we have to possibilities:
- The Reality operator is a perfect shield between the possible and reality
- The Reality operator can give hints of the possible
Therefore, the context is affected by these two ideas, but given that the context can evolve from civilization to civilization, the second possibility is the most likely. However, the reality operator is not easily accessible by simple tools as more of the reality operator is explored deeper and deeper.
How is this context, not the reality operator, impacting the field of Mathematics? After all, as we pointed out, pure math tends to live on the spaces of ideas beyond the context. Therefore, only Applied Mathematics depends on such context, and its impact is two fold:
- If the model does nos predict the context… it is no more Applied Mathematics but pure Math as for example String Theory [3].
- The data from the context is pushing forward the development of Applied Mathematics, given the need to understand and predict the context.
There you have one of its greatest drawbacks, given our limitations on building new sensors, Applied Mathematics requires an access to the context to be able to validate its ideas. However, Applied Mathematics is still lacking on something fundamental, basically to understand the Reality Operator, and although some attempts have been tried, this operator stays still the greatest riddle of the human history.
- Raatikainen, Panu. “Gödel’s incompleteness theorems.” (2013).
- Wahba, Grace. “Three topics in ill-posed problems.” Inverse and ill-posed problems. Academic Press, 1987. 37-51.
- Woit, P “Not Even Wrong: The Failure of String Theory and the Search for Unity in Physical Law Author”